Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 87
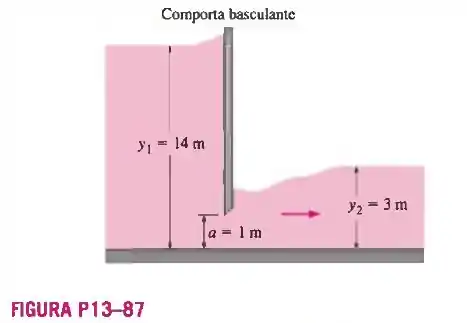
13-87 A água é liberada de um reservatório com 14 m de profundidade em um canal aberto com 6 m de largura através de uma comporta basculante com uma abertura de 1 m de altura no fundo do canal. Se a profundidade do escoamento a jusante dessa comporta for medido como 3 m, determine a taxa de descarga através da comporta.
Passo 1
Vamos lá que o problema já trás um esqueminha no jeito pra a gente!!
A gente quer a taxa de descarga através da comporta, que nada mais é do que a vazão volumétrica, :
Mas não conhecemos !!
Passo 2
Para resolver isso, vamos dar uma espiadinha no livro, na figura 13-38, e pra usar ela vamos recisar de duas relações, a primeira é pra nos localizarmos no eixo :
E a segunda é pra a gente achar uma curva:
Agora traça uma reta vertical no em , acha a curva e vai seguindo ela até ela encontrar a reta que você traçou!!
Fez isso?!
Não da pra saber exaaaaatamente qual é o valor de , mas vamos dizer que é , beleza?!
Substituindo na equação de vazão:
Calculando:
Aweee!