Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 3
A Equação (7.1b) admite que a camada-limite sobre a placa é turbulenta do bordo de ataque para a frente. Imagine um esquema para determinar a espessura da camada-limite com mais precisão quando o escoamento for laminar até um ponto de Rex,crít e turbulento depois disso. Aplique seu esquema para calcular a espessura da camada-limite em x = 1,5 m em um escoamento a 40 m/s de ar a 20°C e 1 atm sobre uma placa plana. Compare seu resultado com a Equação (7.1b). Admita Rex,crít = 1,2 E6.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, a gente tem ar escoando a e e sobre uma placa plana de .
O enunciado então pede que a gente elabore um esquema pra calcular a espessura da camada-limite com uma precisão maior quando ela começa com laminar e muda pra turbulenta. Vamos ver esse esquema aí embaixo:
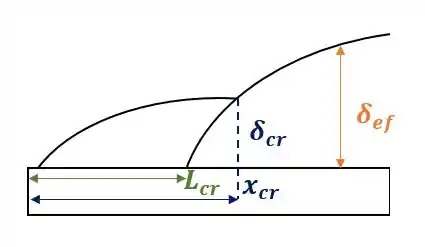
Como vocês podem ver, para a camada-limite laminar, uma distância temos um número de Reynolds crítico de que resulta em uma espessura da camada limite de .
Além disso, neste mesmo ponto, para a cada limite turbulenta com distância , também resultará em e .
Com essas grandezas, iremos calcular a distância efetiva para a qual a camada-limite turbulenta resultará na espessura .
Pra isso, vamos utilizar as seguintes equações para ao espessura da camada-limite:
Além disso, vamos lembrar que para o ar a e , temos e .
Agora vem comigo pra gente resolver essa questão juntos!
Passo 2
Em primeiro lugar, vamos calcular o valor de a partir do número de Reynolds. Sendo assim, teremos:
Agora, com esse valor, podemos calcular facilmente a partir da equação da espessura da camada-limite para o escoamento laminar:
E pra finalizar esse passo, agora vamos calcular a distância do bordo de ataque até o começo da camada-limite turbulenta:
Passo 3
Agora, vamos calcular a distância efetiva . Considerando que o ponto onde a turbulência é medida é , a distância efetiva para a qual a camada-limite turbulenta resultará na espessura :
Agora podemos finalmente calcular o número de Reynolds efetivo :
E pra finalizar esse passo, vamos finalmente calcular , usando a equação para a espessura da camada-limite turbulenta:
Passo 4
Pra finalizar a questão, vamos calcular considerando e comparar esse valor com .
Pra isso, primeiro vamos calcular o número de Reynolds:
Então, a espessura da camada limite será;
Se compararmos essa espessura calculada com a espessura efetiva, nós veremos que elas têm um erro relativo de 28,2%.
Ponto, matamos esse problema juntos!
Resposta
Comparando a espessura calculada sem nenhuma correção com a espessura efetiva , nós veremos que elas têm um erro relativo de 28,2%.