Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 37
Esboce a variação das espessuras das camadas-limite de velocidade e térmica com a distância da aresta frontal de uma placa plana, para o escoamento laminar de ar, água, óleo de motor e mercúrio. Para cada caso, considere uma temperatura média no fluido de 300 K.
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos aqui quatro fluidos (ar, água, óleo de motor e mercúrio) escoando em regime laminar em placas planas a . A partir disso, nós vamos determinar esboços das variações das espessuras das camadas limite fluidodinâmica e térmica com a distância da placa.
Primeiro, podemos determinar uma relação entre as espessuras das camadas limite:
Sendo a espessura da camada limite fluidodinâmica, a espessura da camada limite térmica, o número de Prandtl de cada substância e um expoente empírico.
Portanto, no próximo passo, iremos até algumas tabelas do Apêndice A do livro, onde iremos buscar o número de Prandtl das substâncias e esboçar a “cara” que os gráficos de espessura da camada limite por distância teriam.
Ah, mas antes da gente ir, eu tenho que te falar que esses esboços são feitos olhando a magnitude do valor de para comparar as camadas limite entre si.
Então, vamo lá?
Passo 2
Vamos repetir o processo pra cada um dos fluidos:
- Ar
- Água
- Óleo de motor
- Mercúrio
Para encontrar o número de Prandtl para o ar, devemos ir na Tabela A.4 (página 634). Pra uma temperatura de , .
Sendo assim, . Portanto, a espessura da camada fluidodinâmica é menor que a térmica, como mostra o esboço abaixo:
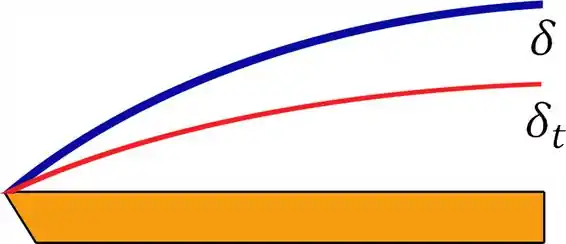
Para encontrar o número de Prandtl para a água, devemos ir na Tabela A.6 (página 640). Pra uma temperatura de , .
Sendo assim, . Portanto, a espessura da camada fluidodinâmica é maior que a térmica, como mostra o esboço abaixo:
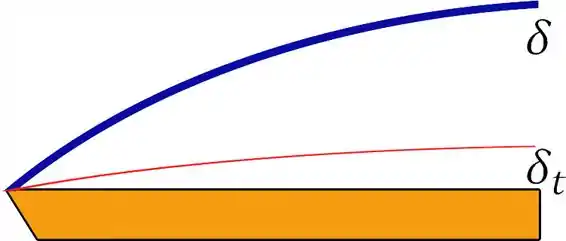
Para encontrar o número de Prandtl para o óleo de motor, devemos ir na Tabela A.5 (página 638). Pra uma temperatura de , .
Sendo assim, . Portanto, a espessura da camada fluidodinâmica é MUITO maior que a térmica, como mostra o esboço abaixo:
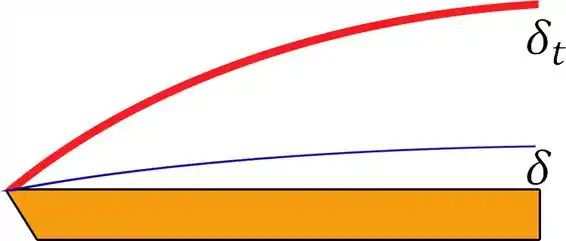
Para encontrar o número de Prandtl para o mercúrio , devemos ir na Tabela A.5 (página 638). Pra uma temperatura de , .
Sendo assim, . Portanto, a espessura da camada fluidodinâmica é MUITO menor que a térmica, como mostra o esboço abaixo:
Pronto, matamos a questão juntos!
Resposta
Ei, a resposta está no passo a passo :)