Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 11

Partindo da correlação de convecção natural com a forma dada pela Equação 9.24, mostre que, para o ar a pressão atmosférica e a uma temperatura do filme de 400   K , o coeficiente de transferência de calor médio para uma placa vertical pode ser estimado por

h L - = 1,40 ∆ T L 1 4                                   10 4 < R a L < 10 9

h L - = 0,98   ∆ T 1 3                                   10 9 < R a L < 10 13

Passo 1

Nessa questão nós temos uma placa vertical com convecção livre com ar à pressão atmosférica e temperatura do filme 400   K . Ou seja,

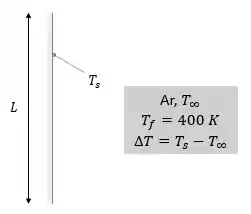
Partindo disso, vamos encontrar a forma de correlação para o coeficiente médio de transferência de calor em termos de ΔT e comprimento característico. Vamos lá!

Passo 2

Para resolver essa questão vamos assumir que o ar é extenso, meio quieto, e tem um comportamento de gás ideal, onde as propriedades do ar foram retiradas da Tabela A.6 para T f = 400   K ,   1   a t m .

Considerando a correlação tendo a forma da Eq. 9.24 com R a L definido,

N u L - = h L - L k = C   R a L n

Onde,

R a L = g β T s - T ∞ L 3 v α = 9,8   m / s 2 1 400 K ∆ T × L 3 26,41 × 10 - 6 m 2 s × 38,3 × 10 - 6 m 2 s = 2,422 × 10 7 ∆ T × L 3

Combinando as duas equações anteriores temos:

h L - = k L C   R a L n = 0,0338 W m . K L C 2,422 × 10 7 ∆ T × L 3 n

Passo 3

Na Fig. 9.6 para condições da camada limite laminar, 10 4 < R a L < 10 9 ,   C   =   0,59 e n   =   ¼ , temos:

h L - = 1,40 L - 1 ∆ T × L 3 1 4 = 1,40 ∆ T L 1 4

Para condições turbulentas na faixa de 10 9 < R a L < 10 13 ,   C   =   0,10 e n   =   1 / 3 , temos:

h L - = 0,98 L - 1 ∆ T × L 3 1 3 = 0,98   ∆ T 1 3

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um coletor solar é constituído por tubo horizontal de cobre de 5c m de diâmetro externo envolto por um tubo de vidro fino concêntrico de 9c m de diâmetro. A água é aquecida à medida que escoa a
Uma caixa eletrônica que consome 200W de potência é resfriada por um ventilador que sopra ar no espaço fechado da caixa. As dimensões da caixa eletrônica são 15c m×50c m× 50c m , e todas as suas su
Um coletor solar é constituído por um tubo horizontal de alumínio de 5c m de diâmetro externo, envolto por um tubo de vidro fino concêntrico de 7c m de diâmetro. A água é aquecida à medida que e
Um tanque esférico de 6m diâmetro interno de aço inoxidável ( k =15W / m ∙ K ) de 1,5c m de espessura é usado para armazenar água com gelo a 0° C na sala a 20° C . As paredes da sala estão també
Reconsiderar Prob.9-41.A fim de reduzir as perdas de calor, propõe-se isolar a tubulação de vapor com isolamento de 5c m de espessura de fibra de vidro ( k = 0,038W / m ∙ K ) e envolvê-la com folha de