Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 16

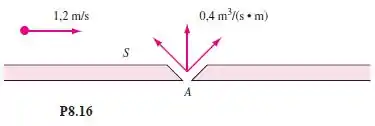
Ar escoa a ao longo de uma superfície plana, quando encontra um jato de ar emitido de uma parede horizontal no ponto , como mostra a Figura . A vazão do jato é por unidade de largura normal ao papel. Se o jato é aproximado por uma fonte não viscosa, (a) localize o ponto de estagnação sobre a parede. (b) A que distância vertical o escoamento do jato se estenderá dentro da corrente.

Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

Como nosso jato é apenas metade de uma fonte, a força equivalente é dada por:

Então seguindo a figura o ponto de estagnação é dado por:

Passo 2

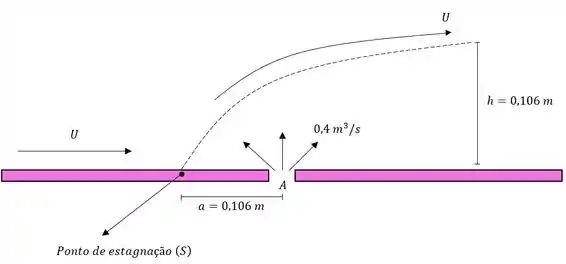
b)

Pra matarmos essa de vez:

Temos de verificar a elevação do escoamento devido ao fluxo no meio das placas, vamos aplicar a formula:

Pra colocar a cereja no bolo se formos esquematizar nosso problema seria assim o resultado:

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para que valor de K / ( U ∞a ) a velocidade no ombro de uma oval de Kelvin será igual a 4 U ∞ ? Qual é a altura h/a dessa oval?

Um cilindro circular é equipado com dois sensores de pressão de superfície para medir p a em θ =180 oep b em θ =105 o . A intenção é usar o cilindro como um anemômetro. Usando a teoria não viscosa, de

Vento a U ∞ e p ∞ escoa em torno de uma cabana Quonset, que é um semicilindro de raio a e comprimento L (Figura P8.48). A pressão interna é pi. Usando a teoria não viscosa, deduza uma expressão para a

Deseja-se simular o escoamento em torno de uma colina ou saliência bidimensional usando uma linha de corrente que passa acima do escoamento sobre um cilindro, como na Figura P8.50. A saliência deve te

Um cilindro é formado por fixação de dois canais semicilíndricos com pinos internos, como mostra a Figura P8.46. Existem 10 pinos por metro de largura de cada lado, e a pressão interna é de 50 kPa (ma