Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 50
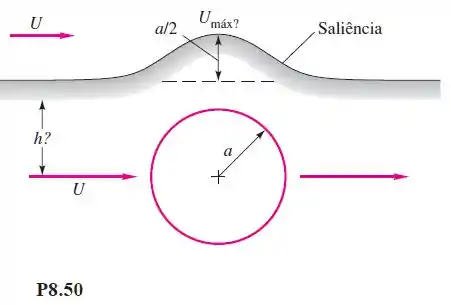
Deseja-se simular o escoamento em torno de uma colina ou saliência bidimensional usando uma linha de corrente que passa acima do escoamento sobre um cilindro, como na Figura P8.50. A saliência deve ter altura igual a a/2, em que a é o raio do cilindro. Qual é a elevação h dessa linha de corrente? Qual é a sobre a saliência comparada com a velocidade U da corrente?
Passo 1
Bora pra mais uma!
Aplicando a equação 8.32, para os dois valores de ângulo, temos:
Sendo , temos:
Dai, obtemos .
A velocidade na saliência (, temos da equação 8.33:
Resposta
h=3a/2 e .
Exercícios de Livros Relacionados
Considere o seguinte campo de velocidade permanente, bidimensional, incompressível: V → = u ,v = - a x 2 i ^ + 2 a x y j ^ , onde a é uma constante. Calcule a pressão em função de x e y.
Um agitador mistura produtos químicos em um grande tanque (Fig. P9–73). A superfície livre do líquido é exposta ao ar ambiente. Os efeitos da tensão superficial são insignificantes. Discuta as condiçõ
Considere o seguinte campo de velocidade permanente, bidimensional, incompressível: V → = u ,v = a x + b i ^ + - a y + c x 2 j ^ , onde a ,bec são constantes. Calcule a pressão em função de x e y.
O óleo de motor à temperatura T = 60 ° C é forçado entre duas placas planas paralelas, permanentes, muito grandes separadas por um espaçamento de altura h = 2,5m m (Fig. P9-77). As dimensões da placa
Considere o escoamento permanente, bidimensional, incompressível devido a um escoamento em espiral de linha de vórtices/sumidouros centrada no eixo z. Na Fig. P9-80 são mostradas linhas de corrente e