Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 46
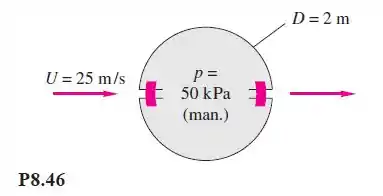
Um cilindro é formado por fixação de dois canais semicilíndricos com pinos internos, como mostra a Figura P8.46. Existem 10 pinos por metro de largura de cada lado, e a pressão interna é de 50 kPa (manométrica). Aplicando a teoria potencial para a pressão externa, calcule a força causada por tensão em cada pino sabendo que o fluido externo é ar ao nível do mar.
Passo 1
Bora pra mais uma!
No nível do mar, temos para o ar Usando Bernoulli para encontrar a pressão na superfície:
Daí, podemos calcular:
Que é bem pequena comparada a força devido à pressão interna, dada por:
Daí pode calcular a força causada por tensão em cada pino:
Resposta
A força é 5060Newton/pino.
Exercícios de Livros Relacionados
Para a película de óleo em movimento descendente do Problema 9–84, encontre uma expressão para a vazão em volume por unidade de largura de óleo descendo pela parede V ˙ L em função de ρ ,μ ,heg . Calc
Considere o escoamento permanente, incompressível, paralelo, laminar de um fluido viscoso descendo entre duas paredes verticais infinitas (Fig. P9–82). A distância entre as paredes é h, e a gravidade
Os dois primeiros termos viscosos no componente θ da equação de Navier -Stokes (Eq. 9-62c) são μ 1 r ∂ ∂ r r ∂ u θ ∂ r - u θ r 2 . Expanda essa expressão o máximo possível usando a regra do produto, p
Um líquido newtoniano incompressível está confinado entre dois cilindros circulares concêntricos de comprimento infinito - um cilindro interno sólido de raio R i e um cilindro oco, permanente, externo
Para o fluido descendo entre duas paredes verticais paralelas (Prob. 9–82), encontre uma expressão para a vazão em volume por unidade de largura V ˙ L em função de ρ ,μ ,heg . Compare seu resultado co