Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 48
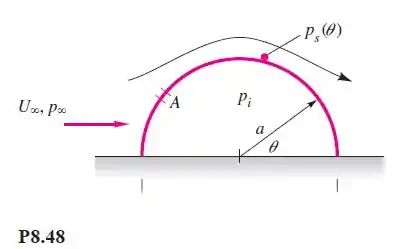
Vento a e escoa em torno de uma cabana Quonset, que é um semicilindro de raio a e comprimento L (Figura P8.48). A pressão interna é pi. Usando a teoria não viscosa, deduza uma expressão para a força para cima sobre a cabana em decorrência da diferença entre e .
Passo 1
Bora pra mais uma!
Esse exercício é similar ao problema 8.46. Se é a pressão de estagnação do nariz (), a distribuição da pressão superficial é:
Então, por meio de integração encontramos a força para cima no meio do cilindro:
Resposta
A força para cima é dada por:
Exercícios de Livros Relacionados
O que são equações constitutivas, e à que equação da mecânica dos fluidos elas são aplicadas?
Defina ou descreva cada tipo de fluido: (a) fluido viscoelástico, (b) fluido pseudoplástico, (c) fluido dilatante, (d) Fluido plástico de Bingham.
Considere um líquido em um tanque cilíndrico. Tanto o tanque quanto o líquido giram como um corpo rígido (Fig. P9–75). A superfície livre do líquido é exposta ao ar ambiente. Os efeitos da tensão supe
O componente r θ do tensor de tensão viscoso em coordenadas cilíndricas é dada por: τ r θ = τ θ r = μ r∂ ∂ r u θ r + 1 r ∂ u r ∂ θ( 1 ) Alguns autores escrevem essa componente como: τ r θ = τ θ r = μ
Repetir Problema 9–73, mas a partir de um quadro de referência que gira com as pás do agitador na velocidade angular ω .