Ar a escoa sobre um longo cilindro, com de diâmetro, que possui um aquecedor elétrico no seu interior. Durante uma bateria de testes foram efetuadas medidas da potência por unidade de comprimento, , necessária para manter a temperatura da superfície do cilindro a , para diferentes velocidades da corrente de ar. Os resultados obtidos são os seguintes:

1. Determine o coeficiente de transferência de calor por convecção para cada velocidade e apresente graficamente os seus resultados.
2. Supondo que o coeficiente convectivo dependa da velocidade de escoamento do ar de acordo com uma relação do tipo , determine os parâmetros e a partir dos resultados da parte (a).

Vamos usar a equação da transferência de calor por convecção, beleza?

Como estamos trabalhando com um cilindro vamos ter:

Nossa tabela nos fornece os valores da potência, que é a nossa transferência de calor, então precisamos encontrar os valores de para cada ponto dela, vamos lá:

Agora vamos montar a tabela, é só a gente ir substituindo os valores de e encontrar cada :

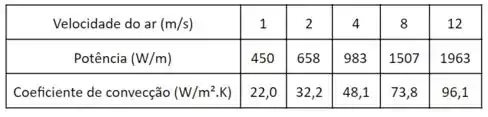
Não temos um aumento linear, pelos números já dá pra perceber e pelo gráfico vemos melhor ainda:

Agora é a vez da letra b!

O exercício quer que a gente encontre os parâmetros e , sendo dada essa relação aqui:

Bom, com os resultados da letra a, nós podemos chutar valores para cada um até obter o que melhor se encaixa… Vamos ver, temos 5 pontos, então vamos montar 5 equações:

Para o nosso primeiro ponto:

Opa! O primeiro já nos deu o valor de , agora vamos substituir no segundo e encontrar o …

Show! Encontramos os parâmetro! Conseguimos!!