Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 129

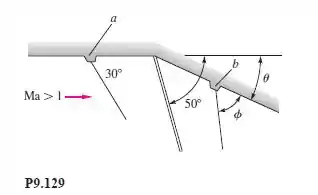
Ar escoa com velocidade supersônica rumo a uma rampa de compressão, como na Figura P9.129. Uma rebarba na parede no ponto a produz uma onda com 30° de ângulo, enquanto o choque oblíquo gerado tem um ângulo de 50°. Qual é (a) o ângulo da rampa, θ , e (b) o ângulo da onda, ϕ , produzido por uma rebarba em b?

Passo 1

Bora pra mais uma!

As duas rebarbas causam as ondas de Mach que estão diretamente relacionadas com o numero de Mach, de forma que:

μ 1 = 30 o →   M a 1 = c o s s e c 30 o = 2 ;   β = 50 o

Daí, a equação 9.86 nos permite obter θ :

  1. θ = tan - 1 ⁡ 2 c o t β M a 1 2 s e n 2 β - 1 M a 1 2 k + c o s 2 β + 2 ≈ 18,13 o

    Daí, sendo M a 2 n = 0,69 = M a 2 s e n 50 o - 18,13 o → M a 2 = 1,307 , conseguimos calcular o ângulo da onda, da forma que:

ϕ = s e n - 1 1 1,307 ≅ 49,9 o

Resposta

  1. θ = 18,13 o
  2. ϕ = 49,9 o
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar escoa em torno de um corpo bidimensional com nariz em forma de cunha, como na Figura P9.128. Determine o semiângulo da cunha, d, para que o componente horizontal da força total de pressão sobre o n
Um escoamento supersônico de ar a M a 1 =3,2ep 1 =50 kPa passa por um choque de compressão seguido por um giro de expansão isentrópica. A deflexão do escoamento é de 30° para cada giro. Calcule M a 2e
O bocal supersônico da Figura P9.138 é superexpandido (caso G na Figura 9.12b) com As/Ag 5 3,0 e uma pressão de estagnação de 350 kPa. Se a borda do jato faz um ângulo de 4° com a linha de centro do b
O escoamento supersônico de ar faz um giro de expansão de 5°, como na Figura P9.141. Calcule o número de Mach e a pressão a jusante, e compare com a teoria de pequenas perturbações.
A solução do Problema 9.122 é M a 2 = 2,750 e p 2 = 145,5 kPa. Compare esses resultados com um giro de compressão isentrópica de 5°, utilizando a teoria de Prandtl-Meyer.