Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 128
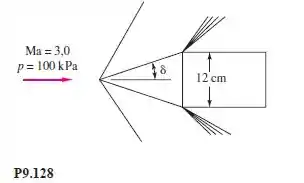
Ar escoa em torno de um corpo bidimensional com nariz em forma de cunha, como na Figura P9.128. Determine o semiângulo da cunha, d, para que o componente horizontal da força total de pressão sobre o nariz seja de 35 kN por metro de profundidade normal ao plano da figura.
Passo 1
Bora pra mais uma!
Independente do ângulo da cunha , a força horizontal é igual ao produto da pressão dentro do choque com a área vertical projetada no nariz:
Da equação 9.38a, temos:
Ou simplesmente:
Por fim, utilizamos a equação para calcular .
Resposta
Exercícios de Livros Relacionados
Em um certo acelerador de partículas, prótons se movem em uma trajetória circular de 23,0m de diâmetro em uma câmara evacuada cujo gás residual está a 295K e a uma pressão de 1,00.10 - 6t o r r . (a)
A 20° C e a uma pressão de 750t o r r , o livre caminho médio do argônio ( A r ) é λ A r = 9,9.10 - 6c m e o livre caminho médio da molécula de nitrogênio ( N 2 ) é λ N 2 = 27,5.10 - 6c m . (a) Determ
As velocidades de 10 moléculas são: 2,0 ; 3,0 ; 4,0 ; … ; 11k m / s . Determine (a) a velocidade média e (b) a velocidade média quadrática das moléculas.
As velocidades de 22 partículas são mostradas a seguir ( N i representa o número de partículas que possuem velocidade v i ):Determine (a) v m é d é , (b) v r m s e (c) v p .
A que temperatura a velocidade média quadrática (a) do H 2 (hidrogênio molecular) e (b) do O 2 (oxigênio molecular) é igual à velocidade de escape da Terra (Ver tabela 13 - 2 )? A que temperatura a ve