Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 141
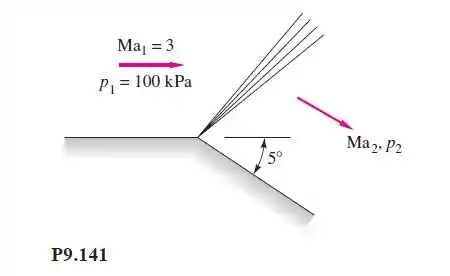
O escoamento supersônico de ar faz um giro de expansão de 5°, como na Figura P9.141. Calcule o número de Mach e a pressão a jusante, e compare com a teoria de pequenas perturbações.
Passo 1
Bora pra mais uma!
Primeiro vamos encontrar para Ma=3 com
Daí
Onde na tabela B.5 lemos
Agora, para calcular a pressão à jusante temos que:
Passo 2
A teoria linear não é muito precisa nesse caso porque mesmo uma volta de apenas é ligeiramente não linear:
Da equação 9.89 temos:
Resposta
O numero de mach e a pressão à jusante são 3,274 e 66,7kPa, em relação à teoria de pequenas perturbações há uma diferença de 9%.
Exercícios de Livros Relacionados
Estime a pressão média na parede frontal de uma quadra de raquetebol, devido às colisões da bola com a parede durante um jogo. Use números razoáveis para a massa da bola, sua velocidade típica e as
A velocidade de escape das moléculas de gás na atmosfera de Júpiter é 60k m / s e a temperatura da superfície de Júpiter é tipicamente - 150 graus Celsius. Calculade as velocidades rms para (a) H 2 (b
Podemos usar v r m s = 3 R T M para calcular as velocidades rms de H2, O2 e CO2 a 123 K e depois comparar essas velocidades com 20% da velocidade de escape em Júpiter para decidir a probabilidade de e
Use o cálculo para mostrar que f ( v ) , dada pela Equação 17-36, tem seu valor máximo em uma velocidade v = 2 k T m .
Ache a temperatura na velocidade rms de uma molécula de hidrogênio, quando a mesma é igual a 343m / s .