Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 146
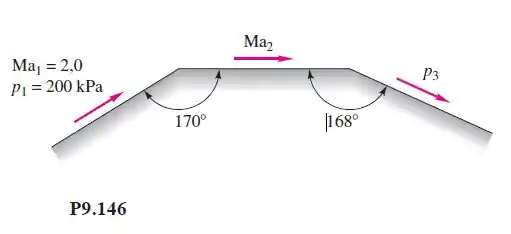
Ar escoa supersonicamente sobre uma superfície que muda de direção duas vezes, como na Figura P9.146. Calcule (a) e (b) .
Passo 1
Bora pra mais uma!
- Na condição inicial, da tabela B.5 lê-se A primeira curva é então que na tabela B.5 lê-se
- A segunda curva é de , logo Na tabela B.5 lê-se Para encontrar a pressão, precisamos da pressão de estagnação que é constante:
Daí:
Resposta
- 2,38
- 47,4kPa
Exercícios de Livros Relacionados
Um gás ideal, cujas moléculas têm massa m , está em equilíbrio térmico à temperatura T dentro de uma ultracentrífuga de raio R que gira com velocidade angular ω . (a) Ache a razão ρ ( R ) / ρ ( 0 ) da
Calcule a razão R entre ⟨ 1 v ⟩ e 1 ⟨ v ⟩ para um gás ideal em equilíbrio térmico.
Num feixe molecular, a densidade de corrente (número médio de moléculas por unidade de área e tempo), para moléculas com velocidades entre v e v + d v , é dada pela (12.3.3). Calcule v p e E p para as
Considere um gás hipotético para o qual a função F ( v ) de distribuição de velocidades [definida na Seção 12.2(d)] tivesse a forma indicada na Fig. P.1. Calcule em função de v 0 : (a) A constante de
Considere um gás ideal de N moléculas, em equilíbrio num recipiente de volume V . Calcule: (a) a probabilidade p 1 de encontrar todas as moléculas concentradas num volume V / 3 (macroestado 1 ); (b) a