Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 142
Um escoamento supersônico de ar a kPa passa por um choque de compressão seguido por um giro de expansão isentrópica. A deflexão do escoamento é de 30° para cada giro. Calcule se (a) o choque é seguido pela expansão e (b) a expansão é seguida pelo choque.
Passo 1
Bora pra mais uma!
A solução desse problema é esboçada abaixo. Uma onda de choque com um giro de é um fluxo extremamente não isentrópico, logo as condições finais não estão perto do original e, também, não concordam entre si.
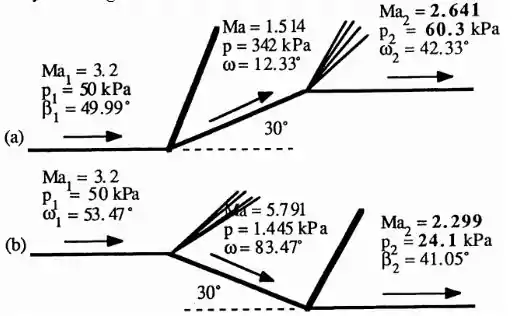
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A velocidade mais provável das moléculas de um gás quando está a uma temperatura T 2 é igual à velocidade média quadrática das moléculas do gás quando está a uma temperatura T 1 . Calcule a razão T 2
Dez partículas estão se movendo com as seguintes velocidades: quatro a 200m / s , duas a 500m / s e quatro a 600m / s . Calcule a velocidade (a) média e (b) média quadrática das partículas. (c) v r m
Dois recipientes estão à mesma temperatura. O primeiro contém gás à pressão p 1 , de massa molecular M 1 e velocidade média quadrática v r m s 1 . O segundo contém gás à pressão 2,0 p 1 , de massa mol
A figura mostra a distribuição de probabilidade da velocidades das moléculas de uma amostra de nitrogênio. A escala do eixo horizontal é definida por v s = 1200m / s . Determine (a) a temperatura do g
Uma molécula de hidrogênio (diâmetro 1,0.10 - 8c m ), movendo-se à velocidade média quadrática, escapa de um forno a 4000K para uma câmara que contém átomos de argônio frios (diâmetro 3,0.10 - 8c m )