Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 47
Um escoamento incompressível bidimensional é dado pelo campo de velocidade , em unidades arbitrárias. Esse escoamento satisfaz a continuidade? Em caso afirmativo, encontre a função corrente e faça um gráfico de algumas linhas de corrente, com setas.
Passo 1
E ai, qual vai ser?! Essa questão temos de resolver! Bora lá então.
Separando esse campo ai vamos ter e , vamos verificar a continuidade, assim:
Sendo então, satisfeita a continuidade.
Vamos então encontrar as linhas de corrente para e , integrando, teremos:
Vamos pegar uns valores arbitrários para traçar as linhas de correntes, peguemos então, , e vai continuando assim, logo, utilizando um software para traçar gráficos, teremos:
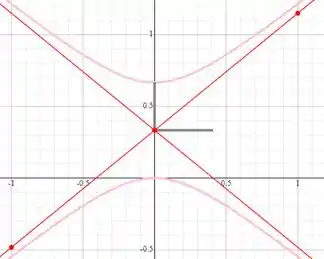
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere o escoamento causado por um vórtice de intensidade K na origem. Calcule a circulação por meio da Equação ( 8.23 ) ao longo de um caminho no sentido horário de r , θ =( a ,0 ) a ( 2 a ,0 ) a
Ar escoa a 1,2m / s ao longo de uma superfície plana, quando encontra um jato de ar emitido de uma parede horizontal no ponto A , como mostra a Figura 8.16 . A vazão do jato é 0,4m 3 / s por unidade d
Trace as linhas de corrente e as equipotenciais do escoamento causado por uma fonte bidimensional de intensidade 3 m em a ,0 mais um sumidouro – m em – a ,0 . Qual é o padrão visto de longe?
Encontre a posição ( x ,y ) sobre a superfície superior do semicorpo na Figura 8.9 a em que a velocidade local iguala a velocidade uniforme da corrente. Qual deve ser a pressão nesse ponto?
Encontre a função corrente e trace algumas linhas de corrente para a combinação de uma fonte 2 m em x ,y = ( + a ,0 ) e uma fonte m em – a ,0 . Existem pontos de estagnação no campo de escoamento?