Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 64

Um escoamento incompressível bidimensional é definido por

u = K y x 2 + y 2

v = K x x 2 + y 2

Em que K = constante. Esse escoamento é irrotacional? Em caso afirmativo, encontre seu potencial de velocidade, faça um esboço de algumas linhas equipotenciais e interprete o padrão de escoamento.

Passo 1

Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos?

Vamos primeiro verificar a velocidade angular, beleza?

2 ω z = ∂ v ∂ x - ∂ u ∂ y = K x 2 + y 2 - 2 K x 2 x 2 + y 2 2 + K x 2 + y 2 - 2 K y 2 x 2 + y 2 2 = 0   ( I R R O T A C I O N A L )

Passo 2

Introduzindo a definição de velocidade potencial e integrando a nossa função, temos que:

u = ∂ ϕ ∂ x = - K y x 2 + y 2

v = ∂ ϕ ∂ y = K x x 2 + y 2

Resolvendo esse sistema para ϕ , vamos ter que: ϕ = K tan - 1 ⁡ y x = K θ

Passo 3

Olha como ficariam algumas linhas equipotenciais para esse problema!!

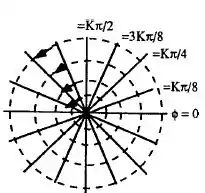
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Investigue o potencial complexo f z = U ∞ ( z + a 2 / z ) e interprete o padrão de escoamento.
Considere o potencial de velocidades em coordenadas polares ϕ = B r 1,2c o s ( 1,2 θ ) , sendo B uma constante. Verifique se ∇ 2 ϕ = 0 . Sendo o caso, encontre a função corrente associada ψ ( r ,θ ) ,
Use o método das imagens para construir o padrão de escoamento de uma fonte 1 m próxima a duas paredes, como mostrado na Figura P 8.72 . Esboce a distribuição de velocidades ao longo da parede inferio
Construa um sistema de imagens para calcular o escoamento de uma fonte a distâncias desiguais de duas paredes, como na Figura P 8.73 . Encontre o ponto de máxima velocidade sobre o eixo y .
Discuta como o padrão de escoamento do Problema P 8.58 pode ser interpretado no sentido da construção de um sistema de imagens para paredes circulares. Por que há duas imagens em vez de uma?