Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 73

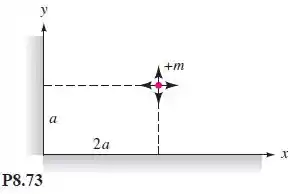
Construa um sistema de imagens para calcular o escoamento de uma fonte a distâncias desiguais de duas paredes, como na Figura P 8.73 . Encontre o ponto de máxima velocidade sobre o eixo y .

Passo 1

E aí, tudo bem? Bora matar essa questão!

Basicamente vamos reproduzir o método da questão anterior, nós a temos aqui no site! Dá uma olhadinha!

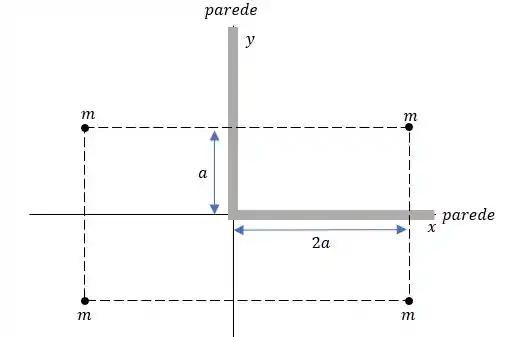
Realizando o espelhamento dos pontos de emissão temos:

Passo 2

Bem, vamos entender nosso escoamento:

Como queremos a velocidade em ao longo da parede:

x > 0 ; y = 0

Fazendo o dimensionamento de acordo com U x temos:

U x = 2 m x + 2 a x + 2 a 2 + a 2 + 2 m x - 2 a x - 2 a 2 + a 2

Só pra entender uma coisinha:

x + 2 a 2 + a 2 = d i s t â n c i a   p a r a   a s   p a r t i c u l a s   e s p e l h a d a s   n o   2 °   e   3 °   q u a d r a n t e

x - 2 a 2 + a 2 = d i s t â n c i a   p a r a   a   p a r t i c u l a   m   e   s u a   e s p e l h a d a   n o   4 °   q u a d r a n t e

A distância é referente à um ponto qualquer no eixo x

Passo 3

Pra matar só precisamos encontrar a velocidade máxima:

Derivando temos:

d U x d x = - 4 m x 6 - 3 a 2 x 4 - 57 a 4 x 2 + 75 a 6 x 2 - 4 a x + 5 a 2 2 x 2 + 4 a x + 5 a 2 2 = 0

Resolvendo esse sistema simples ( s o c o r r o   d e u s ) , temos que:

x ≈ 2,93 a

U m á x = 1,387   m a

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

U x = 2 m x + 2 a x + 2 a 2 + a 2 + 2 m x - 2 a x - 2 a 2 + a 2

x ≈ 2,93 a

U m á x = 1,387   m a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento permanente, bidimensional, incompressível devido a um escoamento em espiral de linha de vórtices/sumidouros centrada no eixo z. Na Fig. P9-80 são mostradas linhas de corrente e
Para a película de óleo em movimento descendente do Problema 9–84, encontre uma expressão para a vazão em volume por unidade de largura de óleo descendo pela parede V ˙ L em função de ρ ,μ ,heg . Calc
Considere o escoamento permanente, incompressível, paralelo, laminar de um fluido viscoso descendo entre duas paredes verticais infinitas (Fig. P9–82). A distância entre as paredes é h, e a gravidade
Os dois primeiros termos viscosos no componente θ da equação de Navier -Stokes (Eq. 9-62c) são μ 1 r ∂ ∂ r r ∂ u θ ∂ r - u θ r 2 . Expanda essa expressão o máximo possível usando a regra do produto, p
Um líquido newtoniano incompressível está confinado entre dois cilindros circulares concêntricos de comprimento infinito - um cilindro interno sólido de raio R i e um cilindro oco, permanente, externo