Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 2
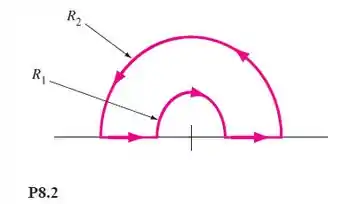
O escoamento plano permanente na Figura tem os componentes de velocidade polares e . Determine a circulação sobre o caminho mostrado.
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
Nosso problema pede pra avaliarmos a circulação no caminho mostrado:
Como se trata de uma integral de caminho precisamos escolher nosso ponto inicial, que tal criarmos um ponto genérico , vamos lá!
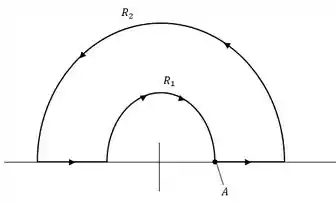
Agora tendo o ponto como referencia vamos fazer percorrer o caminho com a integral de linha, assim:
Rearranjando temos:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
Para a distribuição de velocidade do Problema P4.4, determine se existe uma função corrente e, se existir, encontre uma expressão para ψ ( x , y ) e faça o esboço da linha de corrente que passa pelo p
O veleiro a rotor Flettner na figura E8.2 tem um coeficiente de arrasto na água de 0,006 baseado na área molhada de 4,18 m². Se o rotor gira a 200 rpm, encontre a máxima velocidade do barco que pode s
Modifique o Problema 8.52 como se segue. Para os mesmos dados do veleiro, encontre a velocidade do vento, em km/h, que irá mover o barco a uma velocidade ótima de 4,1 m/s paralela à quilha.
Uma proposta de velocímetro de corrente livre usaria um cilindro com tomadas de pressão em θ = 180 ° e θ = 150 ° . A diferença de pressão daria uma medida de velocidade da corrente livre U ∞ . Contudo
Em princípio, é possível usar cilindros rotativos como asas de avião. Considere um cilindro de 30 cm de diâmetro, girando a 2400 rpm. Ele deve sustentar um avião de 55 kN voando a 100 m/s. Qual deveri