Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 52
O veleiro a rotor Flettner na figura E8.2 tem um coeficiente de arrasto na água de 0,006 baseado na área molhada de 4,18 m². Se o rotor gira a 200 rpm, encontre a máxima velocidade do barco que pode ser atingida com vento de 24 km/h. Qual é o ângulo ótimo entre o barco e o vento?
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!
Olha aí nossa figura E8.2!!
Vamos trazer a nossa memória algumas informações sobre o diâmetro de rotor, o qual tem tamanho de 0,762 m e tem 3,05 m de altura. Além disso, a densidade do ar no nível do mar é de 1,225 kg/m³.
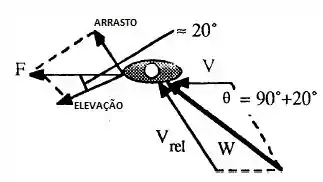
No exemplo 8.2, a gente viu que e . Agora vamos considerar que a velocidade do nosso veleiro seja V e que a velocidade do vendo é W, a velocidade relativa é calculada da seguinte maneira:
Passo 2
Também podemos entender pela física do problema que o “impulso” que o veleiro sente está diretamente relacionado com o arrasto, certo?
Passo 3
Convertendo 24km/h, temos 6,7 m/s. Como mostrado na figura do passo 1, o ângulo entre a elevação causada pelo vento e o arrasto causado por ele, é Então, pela geometria, o ângulo entre a velocidade relativa do vento e do veleiro é . A lei dos cossenos, aplicada no triângulo formado acima vai determinar a velocidade do veleiro.
Passo 4
Para essa condição ótima pedida pelo enunciado, o ângulo entre o vento e a direção do veleiro é: