Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 132

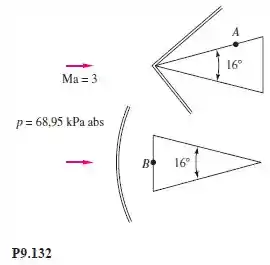
Ar escoa a Ma = 3 e p = 68,95 kPa absoluta com incidência igual a zero rumo a uma cunha com ângulo de 16°, como na Figura P9.132. Se a extremidade aguda estiver para a frente, qual será a pressão no ponto A? Se a extremidade abrupta estiver para a frente, qual será a pressão no ponto B?

Passo 1

Bora pra mais uma!

Sendo Ma=3, obtemos da equação 9.86:

β = 25,61 o  

Então, com a equação 9.83a:

  1. P A P 1 = 2,8 3 s e n 25,61 o 2 - 0,4 2,4 = 1,8 → P A = 68,95 k P a * 1,8 = 124,11 k P a

  2. Um choque normal ocorre, e p B = p o 2 dentro do choque. Sendo p o 1 = p 1 0,0272 = 2534,9 k P a , da tabela B.2, obtemos:

p o 2 p o 1 = 0,3283 ,   e n t ã o   p o 2 = 0,3283 * 2534,9 k P a = 832,22 k P a

Resposta

  1. 124,11kPa
  2. 832,22kPa.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma compressão isentrópica suave de 20° de giro, como mostra a Figura P9.144. As ondas de Mach assim geradas formarão um leque convergente. Esboce esse leque com a maior exatidão possível, u
Ar escoa supersonicamente sobre uma superfície em arco de círculo, como na Figura P9.148. Calcule (a) o número de Mach M a 2 e (b) a pressão p 2 assim que o escoamento deixa a superfície circular.
Ar escoa supersonicamente sobre uma superfície que muda de direção duas vezes, como na Figura P9.146. Calcule (a) M a 2 e (b) p 3 .
O escoamento de ar a M a 1 = 3,2 passa por uma deflexão de choque oblíquo de 25°. Que giro de expansão isentrópica é necessário para trazer o escoamento de volta para (a) M a 1 e (b)p 1 ?
Um bocal convergente-divergente com razão de área de saída 4:1 e p 0 = 500 kPa, como na Figura P9.147, opera em uma condição subexpandida (caso I da Figura 9.12b). A pressão do recipiente é p a = 10 k