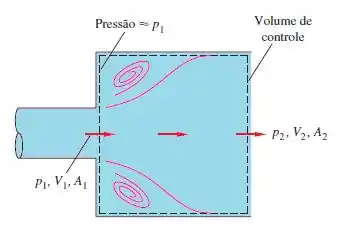
Quando o escoamento em um tubo se alarga bruscamente de A1 para A2, como mostrado abaixo, aparecem turbilhões de baixa velocidade e baixo atrito nos cantos, e o escoamento gradualmente se alarga até A2 a jusante. Usando o volume de controle sugerido, admitindo escoamento permanente e incompressível, considerando que na seção anular dos cantos (como mostrado), mostre que a pressão a jusante é dada por:

Despreze o atrito na parede.

Vamos olhar agora pro nosso balanço de pressões em torno do nosso volume de controle!!

Note que as pressões na parede que serão canceladas são apenas aquelas que estão na base e no topo do VC, as outras não, ou seja, isso dará para gente um balanço de forças como sendo:

Bem, agora vamos lembrar que a vazão mássica deve ser mantida uma vez que se trata de um escoamento incompressível e permanente, então:

Substituindo entro do nosso balanço de forças na direção X:

Vamos agora fazer uma relação de V2 com V1, porque a equação que precisamos encontrar é função apenas de V1.

Agora, vamos só ajustar nossa equação para termos a equação que desejamos!!

Mas quem é essa bendita pressão na parede na nossa equação, afinal ela não aparece na nossa equação. Aí aqui vai o pulo do gato da questão, precisamos considerar que a pressão da parede deve ser igual a pressão , afinal se você for observar bem, as pressões que influenciam além de seria a pressão atmosférica, que é provavelmente bem menor que a pressão 1, podendo então dizer que implicando em