Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 71

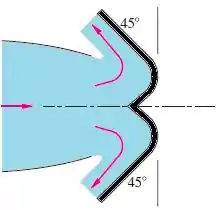
Suponha que um defletor é estendido na saída do motor a jato do problema 3.50, como mostrado na figura abaixo. Qual será agora a força de reação Rx sobre a bancada de testes? Será essa reação suficiente para servir como força de frenagem durante a aterrisagem de um avião?

Passo 1

E aí, gente!! Tudo bem? Vamos que vamos encarar mais um desafio de mecânica dos fluidos?

Bem, como ele está fazendo referência ao problema 3.50, vamos pegar os dados do enunciado desse problema.

Passo 2

Vamos selecionar quem será nosso volume de controle, beleza? Ele deve englobar todo nosso sistema!!!

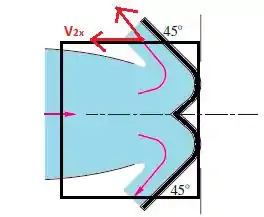
Vamos adotar que nosso eixo x cresce para direita e nosso eixo y para cima. Logo, temos uma força contrária, uma força de vazão que está no sentido do nosso eixo x crescendo e perceba que também precisamos levar em consideração a contribuição da vazão de saída, e que como a velocidade no ponto 2 é inclinada, vamos precisar decompor essa velocidade 2, certo?

Passo 3

Substituindo os valores, e lembrando que como a vazão deve ser mantida e assumindo que a velocidade de saída continua sendo 900 m/s!

Ou seja, é uma força direcionada para esquerda do nosso volume de controle!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma camada bidimensional de água, com 10 cm de espessura e movendo-se a 7 m/s, colide com uma parede fixa inclinada 20° com relação à direção da camada. Considerando escoamento sem atrito, encontre (a

Ar a 20°C e 1 atm escoa em um duto de 25 cm de diâmetro a 15 m/s, como na Figura P3.84. Na saída, o ar atinge um cone de 90°, como mostra a figura. Calcule a força do escoamento de ar sobre o cone.

Para a bomba de jato de água do Problema P3.36, adicione os seguintes dados: p 1 = p 2 = 172,4k P a e a distância entre as seções 1 e 3 é de 2 m. Se a tensão de cisalhamento média na parede entre as s

O barco da figura P3.88 tem propulsão a jato por uma bomba que desenvolve uma vazão Q e ejeta água pela popa à velocidade V j . Se a força de arrasto sobre o barco for F = k V 2 , em que k é uma const

Um jato de fluido de diâmetro D 1 entra em uma grade de pás móveis à velocidade absoluta V 1 e ângulo β 1 , e sai à velocidade absoluta V 2 e ângulo β 2 , como na Figura P3.78. As pás movem-se à veloc