Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 64

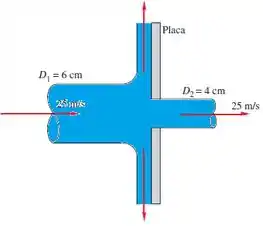
O jato d´água de 6 cm de diâmetro a 20°C da figura abaixo atinge uma placa contendo um orifício de 4 cm de diâmetro. Parte do jato atravessa pelo orifício, e parte é defletida. Determine a força necessária para conter a placa.

Passo 1

Bem, antes de começar, quero saber se você está bem! Então vamos que vamos para mais um desafio de MecFlu?

Primeira coisa que vamos fazer é delimitar nosso volume de controle como abaixo!!!

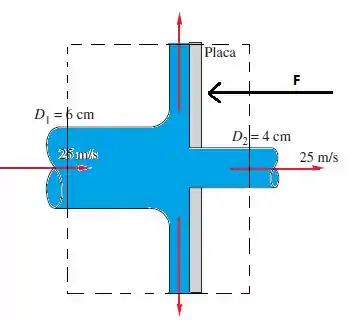
Ao aplicarmos nosso balanço de forças então no nosso volume de controle, a gente vai observar que:

m ˙ 1 V 1 - F - m ˙ s o b e V s o b e + m ˙ d e s c e V d e s c e + m ˙ 2 V 2 = 0

Passo 2

Conhecemos os diâmetros e velocidades dos pontos 1 e 2 do nosso volume de controle, e, portanto, conhecemos também as vazões volumétricas, certo?

Q 1 = V 1 A 1 = 25 π 4 0,06 2 = 0,0707   m 3 / s

Q 2 = V 2 A 2 = 25 π 4 0,04 2 = 0,0314   m 3 / s

Passo 3

Reescrevendo nosso balanço de forças de tal forma que consigamos isolar F, temos:

m ˙ 1 V 1 - F - m ˙ s o b e V s o b e + m ˙ d e s c e V d e s c e + m ˙ 2 V 2 = 0

- F = m ˙ s o b e V s o b e + m ˙ d e s c e V d e s c e + m ˙ 2 V 2 - m ˙ 1 V 1

Bem, aqui vai o pulo do gato da questão!! Você percebeu que o enunciado não disse NADA sobre as vazões que saem por cima e por baixo após baterem na nossa placa, certo? Ele disse isso porque provavelmente essas vazões são desprezíveis quando comparadas as vazões de entrada e saída, o que pode nos gerar a simplificação no nosso balanço de forças, tal que:

- F = 0 + 0 + ρ Q 2 V 2 - ρ Q 1 V 1 = ρ Q 2 V 2 - Q 1 V 1 = 998 0,0314   x   25 - 0,0707   x   25

F = 784 - 1764 = - 980   N

Resposta

F = - 980   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reverta o escoamento na Figura P3.116, de modo que o sistema passe a operar como uma turbina de fluxo radial. Considerando que o escoamento na seção de saída 1 não tem velocidade tangencial, deduza um
Retome a grade de turbina do Problema P3.78 e deduza uma fórmula para a potência P desenvolvida, usando o teorema da quantidade de movimento angular da Equação (3.55).
O irrigador de gramados horizontal da Figura P3.110 tem uma vazão d’água de 15,2 L/min, introduzida verticalmente pelo centro. Calcule (a) o torque resistente necessário para manter os braços sem rota
Admita que o foguete com propelente sólido do problema P3.35 seja montado em um carro de 1000 kg para propulsioná-lo por um longo aclive de 15°. O motor de foguete pesa 900 N, incluindo 500 N de prope
Água a 20°C escoa a 114 L/min através do tubo de 19 mm de diâmetro com duas curvas, como na Figura P3.115. As pressões são p 1 = 206,84k P aep 2 = 165,47k P a . Calcule o torque T no ponto B necessári