Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 60

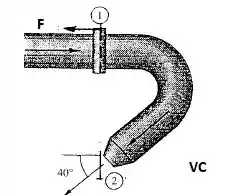
Água a 20°C escoa através do cotovelo da figura abaixo e descarrega para atmosfera. O diâmetro do tubo é D 1 = 10   c m , enquanto que D 2 = 3   c m . Para uma vazão em peso de 150 N/s, a pressão p 1 = 2,3   a t m (manométrica). Desprezando o peso da água e do cotovelo, calcule a força sobre os parafusos dos flanges na seção 1.

Passo 1

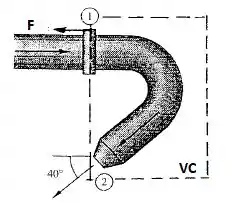
Fala ae, galera! Bora que bora para mais um desafio? Vamos primeiramente definir nosso volume de controle como mostrado abaixo!!

Primeiro vamos mudar essa vazão em peso aí para uma unidade mais “bonitinha” e que estamos mais acostumados, beleza?

Q = V a z ã o   e m   p e s o g   x   ρ = 150 10   x   979 = 0,0153   m 3 / s  

Passo 2

Vamos olhar o seguinte, agora precisamos aplicar um balanço de forças em volta do nosso volume de controle pra conseguirmos identificar qual será a força F necessária, ok?

∑ F x = - F + p 1 A 1 = m ˙ 2 u 2 - m ˙ 1 u 1

Lembrando que para um escoamento incompressível e permanente, temos que as vazões 2 e 1 são iguais e mais ainda, precisamos lembrar que a velocidade na saída está inclinada, isso quer dizer que vamos precisar decompor para encontrar a componente x.

- F + p 1 A 1 = m ˙ V 2 x - V 1

Decompondo a velocidade 2, temos que V 2 x = - V 2 c o s θ ! Lembrando que o sinal negativo é porque a componente x está direcionada para o sentido contrário e usual que adotamos sempre para o eixo x crescendo, beleza?

- F + p 1 A 1 = m ˙ - V 2 c o s θ - V 1

- F + p 1 A 1 = ρ A 1 V 1 - V 2 c o s θ - V 1

Passo 3

Okay, estamos quase terminando tudo!!! Mas precisamos encontrar nossas velocidades V1 e V2 e isso é tranquilo, porque encontramos lá no passo 1 qual era a vazão volumétrica do nosso escoamento, então temos que:

V 1 = Q A 1 = 0,0153 π 4 0,1 2 = 1,95   m / s

V 2 = Q A 2 = 0,0153 π 4 0,03 2 = 21,7   m / s

Agora é jogar tudo no balanço e ser feliz hehe

F = p 1 A 1 + ρ A 1 V 1 V 2 c o s θ + V 1

F = 2,3   x   101350 π 4 0,1 2 + 998 π 4 0,1 2 1,95 21,7 c o s 40 ° + 1,95 = 2100   N

Resposta

F = 2100 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura P3.87 simula um escoamento com múltiplas derivações, com o fluido sendo removido por uma parede porosa ou por um trecho perfurado do tubo. Admita escoamento incompressível com atrito desprezí
Um rio de largura b e profundidade h 1 passa sobre um obstáculo submerso, ou “vertedouro afogado”, Figura P3.80, emergindo em uma nova condição de escoamento V 2 , h 2 . Despreze a pressão atmosférica
O modelo de carro da Figura P3.82 pesa 17 N e deve ser acelerado a partir do repouso por um jato de água de 1 cm de diâmetro à velocidade de 75 m/s. Desprezando o arrasto do ar e o atrito das rodas, c
Ar a 20°C e 1 atm em um tubo entra no fundo de um medidor de vazão cônico de 85°, com um fluxo de massa de 0,3 kg/s, como mostra a Figura P3.79. O escoamento anular permanente é capaz de suportar um c
A placa de orifício da Figura P3.85 causa uma grande queda de pressão. Para o escoamento d’água a 20°C de 1893 L/min, com diâmetro do tubo D = 10c m e do orifício d = 6c m ,p 1 - p 2 ≈ 145k P a . Se o