Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 68

O foguete da figura abaixo tem uma descarga supersônica, e a pressão de saída p s não é necessariamente igual a p a . Mostre que a força F requerida para conter esse foguete na bancada de teste é de F = ρ s A s V s 2 + A s p s - p a . Será essa força aquela que chamamos de empuxo do foguete?

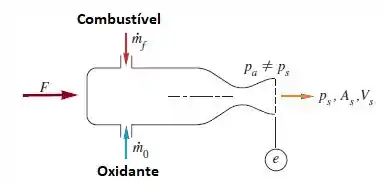
Passo 1

Fala aí, galerinha!!! Vamos encarar mais um exercício?

Vamos de início fazer um volume de controle apropriado para começar a fazer nosso balanço de forças.

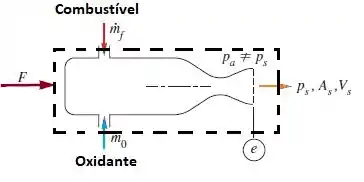
Passo 2

Bem, se observamos bem, temos as forças relacionadas as vazões e a própria força F que está na direção crescente do eixo X. Vale lembrar que toda vazão que estiver entrando no nosso volume de controle terá sinal positivo e o caso esteja saindo, terá sinal negativo. Se subtrairmos a pressão p a em todos os lados do nosso volume de controle, teremos que apenas a saída terá p ≠ 0 .

∑ F x = F - p s - p a A s + m ˙ 0 u 0 , x + m ˙ f u f , x - m s ˙ u s = 0

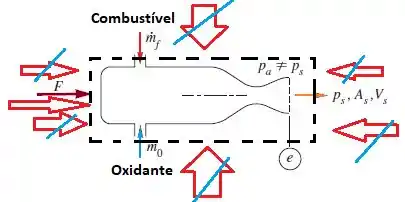
Note que não há componente x tanto para a velocidade relacionada a entrada de oxidante e de combustível, portanto suas componentes serão zero!!!

∑ F x = F - p s - p a A s - m s ˙ u s = F - p s - p a A s - m s ˙ V s

Passo 3

Sabemos que a vazão no ponto “e” será dado por: m ˙ s = ρ s A s V s

Então se isolarmos F, vamos ter nossa equação da seguinte forma:

F = ρ s A s V s 2 + p s - p a A s

Essa é a força de empuxo que “empurra” o foguete!!!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a Figura P3.36 como um problema geral de análise de uma bomba ejetora de mistura. Se todas as condições ( p ,ρ ,V ) são conhecidas nas seções 1 e 2 e se o atrito na parede é desprezível, ded
Um tanque alto descarrega através de um orifício circular, como na Figura P3.95. Use a fórmula de Torricelli do problema P3.81 para calcular a velocidade de saída. (a) Se, nesse instante, a força F ne
Um jato líquido de massa específica ρ e área A atinge um bloco e se divide em dois jatos, como na Figura P3.75. Considere a mesma velocidade V para os três jatos. O jato superior sai com um ângulo θ e
o carrinho da Figura P3.107 move-se à velocidade constante V 0 = 12m / s e coleta água com uma concha de 90 cm de largura que se aprofunda h = 2,5c m em um lago. Despreze o arrasto do ar e o atrito da
Modifique o Exemplo 3.15, de modo que o braço parta do repouso e acelere até sua velocidade final de rotação. O momento de inércia do braço em relação a O é I o . Desprezando o arrasto do ar, encontre