Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 134
O escoamento em um tubo pode alternar entre os regimes laminar e turbulento para números de Reynolds na zona de transição. Projete uma bancada de testes consistindo de um cilindro transparente de plástico de nível constante (altura de carga constante) com graduação de profundidade e um trecho de tubo de plástico (admitido liso) conectado à base do cilindro, através do qual escoa água para um recipiente de medição. Selecione as dimensões do tanque cilíndrico e do tubo de modo que o sistema seja compacto, mas que opere na faixa de transição. Projete o experimento de modo que você possa facilmente variar a altura de carga no tanque de um nível baixo (escoamento laminar) até níveis da zona de transição para escoamento turbulento, e viceversa. (Escreva instruções para os estudantes reconhecerem quando o escoamento é laminar ou turbulento.) Gere curvas (sobre um mesmo gráfico) da profundidade do tanque versus número de Reynolds, considerando escoamento laminar ou turbulento.
Passo 1
Oi pessoal, tudo bem ?
Bem, para encontrar a faixa de valores para a profundidade requerida no reservatório de água para criar escoamento em um tubo liso, deve-se lembrar primeiramente da equação da energia:
Para o experimento proposto, vamos considerar as perdas de carga representadas pelas eq da perda de carga maior e menor:
Passo 2
Considerações: Consideramos que
Estima-se que
E dizemos que
O fator de atrito pode ser dado de duas formas diferentes:
), quando o escoamento for turbulento;
, quando o escoamento for laminar.
E o número de Reynolds (Re) é dado pela expressão:
Por sua vez, a relação entre a vazão e a velocidade é:
Passo 3
Rearranjando os termos da eq da energia, com as considerações feitas:
Então, como todas as expressões interdependem entre si, ao variar os valores das vazões no reservatório, haverá uma variação em cadeia: primeiro da velocidade, depois do Re, depois do coeficiente de atrito, até a profundidade do tanque.
Valores a serem considerados:
| | ( se escoamento turbulento) ou ( se escoamento laminar | | | rugosidade (Tubo liso) e
Passo 4
Colocando os valores ordenados no Excel com suas respectivas fórmulas, e utilizando a ferramenta Solve, é possível encontrar a variação de velocidades e os números de Reynolds correspondentes em relação à variação de vazão, como mostra a tabela a seguir:
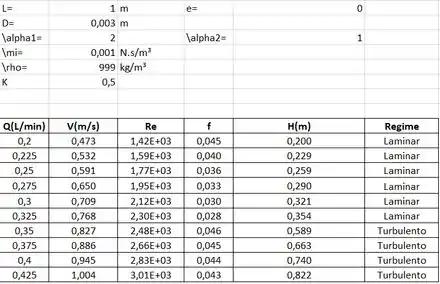
Vale ressaltar que, com base no gráfico feito, desde o valor da vazão de 0,02 L/min até 0,0325 L/min, o fator de atrito recebe o valor proveniente de:
, pois o escoamento é laminar (Re
A partir daí o valor de f é proveniente de:
), pois o escoamento é turbulento (Re>2300);
Assim, o gráfico do número de Reynolds versus a cabeça de reservatório necessária:
Resposta
As taxas de fluxo são realistas e podem ser facilmente medidas usando um sistema de tanque / temporizador. A cabeça necessária também é realista para um experimento de laboratório em pequena escala em torno de Re = 2300, o fluxo pode oscilar entre laminar e turbulento:
Quando a turbulência é acionada (quando H> 0,353 m), a resistência ao fluxo aumenta
requerendo H> 0,587 m para manter; daí o fluxo reverter para laminar, apenas para tropeçar
novamente a turbulento! Esse comportamento será visível: o fluxo de saída retornará e
adiante entre liso (laminar) e caótico (turbulento)