Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 107

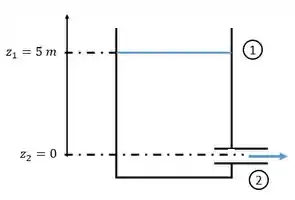
Um tanque de água (aberto para a atmosfera) contém água a uma profundidade de 5 m. Um furo com diâmetro de 25 mm é perfurado no fundo. Modele o furo como de borda-viva, e estime a vazão (L/s) que sai do tanque. Se você fixar um pequeno trecho de tubo no furo, de quanto mudaria a vazão? se em vez disso, você polir a saída do furo, arredondando as bordas (r = 5 mm), de quanto mudaria a vazão?

Passo 1

Neste problema será calculada a vazão de um escoamento considerando diferentes situações de entrada do duto. Para isso será avaliada a velocidade do escoamento como função do coeficiente de perda de carga.

A Equação da Energia será utilizada na forma:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

Sendo a perda de carga total definida como:

h l T = f L D V 2 2   2   + K V 2 2 2

Como hipótese e dados do enunciado tem-se que;

- regime permanente ( ∂ / ∂ t = 0 );

- z 1 = 5   m ;

- z 2 = 0 ;

- escoamento incompressível ( ρ 1 = ρ 2   e ρ a r = 1,23   k g / m 3 );

- α ≈ 1,0 ;

- D = 25   m m ;

- V 1 ≈ 0 (reservatório com grandes dimensões);

- p 1 = p 2 = 0 (pressão atmosférica em termos manométrico);

- ρ á g u a = 1000   k g / m 3 ;

- L ≈ 0 , lo perdas por atrito são desprezíveis comparadas com as perdas de entrada e de saída:

h l T = f L D V 2 2   2 ⏞ ≈ 0   + K V 2 2 2

h l T =   K V 2 2 2

Passo 2

Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l T

p 1 ρ - p 2 ρ = α V 2 2 2 - α V 1 2 2 + g ( z 2 - z 1 ) + h l T

p 1 - p 2 ρ = α V 2 2 - V 1 2 2 + g z 2 - z 1 + h l T

Sabendo a expressão de h l T , que z 2 = 0 , V 1 ≈ 0 , α ≈ 1 e p 1 = p 2 = 0 :

0 = V 2 2 2 - g z 1 + K V 2 2 2

2 g z 1 = V 2 2 1 + K

Logo a expressão da velocidade é dada por:

V 2 2 = 2 g z 1 1 + K

V 2 = 2 g z 1 1 + K

Passo 3

Obtendo o coeficiente de perda de carga para diferentes configurações da entrada do tubo segundo Tabela 8.2:

- Borda-viva

K = 0,5

- Borda com reentrada

K = 0,78

- Borda arredondada ( r / D = 5 / 25 = 0,2 )

K = 0,04

Passo 4

Logo as velocidades das diferentes situações serão:

- Borda-viva

V 2 = 2 g z 1 1 + K

V 2 = 2 × 9,81 × 5 1 + 0,5

V 2 = 8,09   m / s

- Borda com reentrada

V 2 = 2 × 9,81 × 5 1 + 0,78

V 2 = 7,42   m / s

- Borda arredondada

V 2 = 2 × 9,81 × 5 1 + 0,04

V 2 = 9,71   m / s

Passo 5

A vazão será dada por:

Q = V 2 A 2

Q = V 2 π D 2 2 4

Considerando as situações de avaliação:

- Borda-viva

Q B V = 8,09 × π × 25 × 10 - 3 2 4

Q B V = 3,97 × 10 - 3   m 3 / s

- Borda com reentrada

Q B R = 3,64 × 10 - 3   m 3 / s

- Borda arredondada

Q B A = 9,71 × π × 25 × 10 - 3 2 4

Q B A = 4,77 × 10 - 3   m 3 / s

Passo 6

- Diferença de vazão entre borda viva e com reentrada:

∆ Q = Q B R - Q B V

∆ Q = 3,64 × 10 - 3 - 3,97 × 10 - 3

∆ Q = -   0,33 × 10 - 3   m 3 / s

Ao substituir a borda vida por borda com reentrada há queda da vazão de 0,33 L/s.

- Diferença de vazão entre borda viva e arredondada:

∆ Q = Q B A - Q B V

∆ Q = 4,77 × 10 - 3 - 3,97 × 10 - 3

∆ Q = 0,8 × 10 - 3   m 3 / s

Ao substituir a borda vida por borda arredondada há aumento da vazão de 0,8 L/s.

Resposta

Q B V = 3,97 × 10 - 3   m 3 / s

- Diferença de vazão entre borda viva e com reentrada:

∆ Q = -   0,33 × 10 - 3   m 3 / s

- Diferença de vazão entre borda viva e arredondada:

∆ Q = 0,8 × 10 - 3   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em Pequelândia, as casas tem menos de 30 cm de altura! A chuva cai em regime laminar! O tubo de drenagem da figura abaixo tem apenas 2 mm de diâmetro. (a) Quando a calha está cheia, qual é a taxa de d
Um óleo (d = 0,9) escoa pelo tubo da figura abaixo com Q = 0,99m 3 / h . Qual é a viscosidade cinemática do óleo em m²/s? O escoamento é laminar?
Para endireitar e suavizar o escoamento de ar em um duto de 50 cm de diâmetro, ele é equipado com uma “colmeia” de tubos finos de 30 cm de comprimento e 4 mm de diâmetro, como mostrado abaixo. O escoa
Óleo SAE 30 a 20°C escoa no tubo de 3 cm de diâmetro da figura abaixo que está inclinado a 37°. Para as medidas de pressão mostradas, determine (a) se o escoamento é para cima ou para baixo e (b) a va
Um elemento de escoamento laminar (EEL) (Meriam Instrumento Co.) mede pequenas vazões de gás com um feixe de tubos ou dutos capilares agrupados no interior de um grande tubo externo. Considere oxigêni