Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 151
Para o escoamento no tubo do reservatório do Exemplo 8.5, considere o efeito da rugosidade do tubo sobre a vazão, considerando que a pressão da bomba seja mantida a 153 kPa. Trace o gráfico da vazão volumétrica em função da rugosidade do tubo desde o caso de tubo liso (e = 0) até a situação em que a rugosidade é muito grande (e = 3,75 mm). Considere também o efeito do comprimento do tubo (novamente considerando que a bomba produza sempre 153 kPa) para um tubo liso. Trace o gráfico da vazão volumétrica em função do comprimento do tubo desde L = 100 m até L = 1000 m.
Passo 1
Oi pessoal, tudo bem ?
Bem, para encontrar a faixa de valores para a profundidade requerida no reservatório de água para criar escoamento em um tubo liso, deve-se lembrar primeiramente da equação da energia:
Consideremos ;
;
As perdas de carga serão representadas pela eq da perda de carga maior, e a eq perda de carga menor será desconsiderada:
Passo 2
Do exemplo 8.5, temos:
Obs: propriedades da água à , Tabela A.8 .
De acordo om as considerações, a equação da energia, de forma simplificada, fica:
O fator de atrito pode ser dado de duas formas diferentes:
), quando o escoamento for turbulento;
Porém, como o tubo é liso, , então:
,
, quando o escoamento for laminar.
E o número de Reynolds (Re) é dado pela expressão:
Por sua vez, a relação entre a vazão e a velocidade é:
Passo 3
Caso 1) Fazer o gráfico da vazão volumétrica em função da rugosidade do tubo desde o caso de tubo liso (e = 0) até a situação em que a rugosidade é muito grande.
Então, como todas as expressões interdependem entre si, ao variar o valor da rugosidade relativa, haverá uma variação em cadeia.
Colocando os valores ordenados no Excel com suas respectivas fórmulas, e utilizando a ferramenta Solve, é possível determinar os valores antes desconhecidos, como mostra a tabela a seguir:
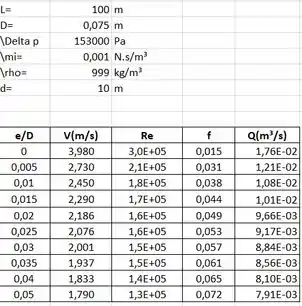
Assim, o gráfico da variação da vazão versus rugosidade relativa fica:
Não é possível enrugar o tubo o suficiente para diminuir a velocidade o fluxo até um fluxo laminar para este Δp.
Passo 4
Caso 2) Traçar o gráfico da vazão volumétrica em função do comprimento do tubo desde L = 100 m até L = 1000 m.
Novamente, colocando os valores ordenados no Excel com suas respectivas fórmulas, e utilizando a ferramenta Solve, é possível determinar os valores antes desconhecidos, como mostra a tabela a seguir:
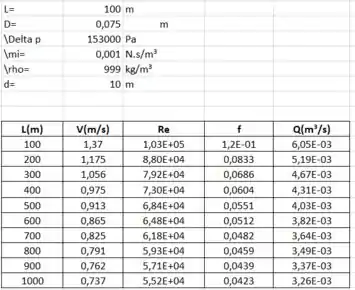
Assim, o gráfico da variação da vazão versus comprimento relativa fica:
Resposta
Ei, a resposta está no passo a passo :)