Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 80
Uma esfera pesada fixada em uma corda se deslocaria um ângulo θ quando imersa em uma corrente de velocidade U, como na Figura P7.80. Deduza uma expressão para u em função das propriedades da esfera e do escoamento. Qual o valor de θ se a esfera for de aço (d = 7,86) de 3 cm de diâmetro e o escoamento for de ar padrão ao nível do mar com U = 40 m/s? Despreze o arrasto da corda.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma esfera de aço () de diâmetro fixada em uma corda, que se desloca um ângulo quando imersa em uma corrente de ar de velocidade , como demonstra a figura que ilustra a questão.
A questão nos pede pra encontrar uma expressão para , e pra isso a gente vai ter que descobrir quais forças atuam nesse sistema.
Nos próximos passos, a gente vai descobrir como relacionar as forças atuando nesse sistema e usá-las pra encontrar uma expressão para , além de calcular o valor numérico correspondente.
Pra isso vamos lembrar que para o ar a a massa específica é e a viscosidade .
Pronto, vamos resolver essa questão juntos!
Passo 2
Em primeiro lugar, vamos entender quais forças estão atuando no sistema. Pra isso, vamo olhar esse esquema abaixo:
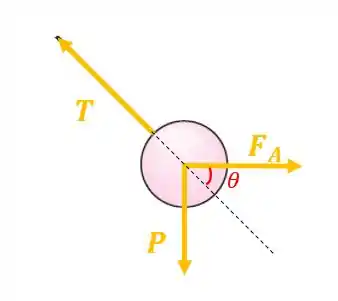
Temos então, a tração da corda , o peso da esfera e a força de arrasto do escoamento.
Como dá pra notar, temos um triângulo retângulo sendo formado entre as forças e . Basta que a gente faça uma relação trigonométrica simples:
A força de arrasto pode ser calculada como:
Sendo: o coeficiente de arrasto da geometria; e , a área da esfera.
Além disso, o peso , já considerando o empuxo causado pelo ar, pode ser calculado como:
Sendo: a aceleração da gravidade e o volume da esfera.
Logo, nossa expressão pra se torna:
Passo 3
Pra resolver a questão, devemos calcular o coeficiente de arrasto .
Pra isso, primeiro temos que calcular o número de Reynolds:
Sendo assim, vamo na Figura 7.16 (b) na página 492:
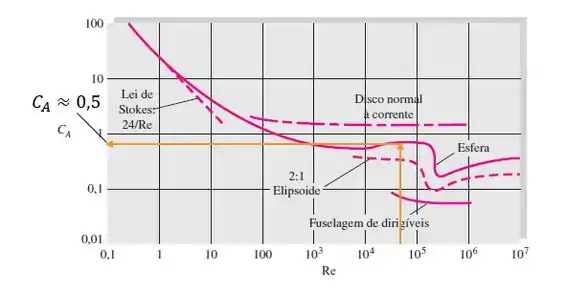
E achamos .
Agora podemos finalizar a questão e calcular :
Pronto, matamos a questão juntos!
Resposta
O ângulo que a esfera desloca a corda é