Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 73
Uma esfera de vidro cal-soda de diâmetro é encapsulada em uma casca esférica de baquelita de espessura . A esfera composta está inicialmente a uma temperatura uniforme, , e é exposta a uma fluido com, com Determine a temperatura no centro do vidro em . Despreze a resistência térmica de contato na interface entre os dois materiais.
Passo 1
Vamo lá galera! As difusividades térmicas da baquelite e do vidro são,
Como , é razoável atribuir uma difusividade térmica uniforme de para a esfera composta. Como e a resistência de contacto térmico entre o vidro e a baquelite é insignificante, podemos tratar a esfera composta como uma única esfera de diâmetro com propriedades uniformes. O número Biot para a esfera simples é
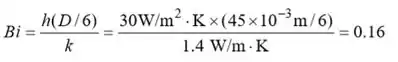
Passo 2
Portanto, a aproximação da capacitância não é válida. O número de Fourier é,
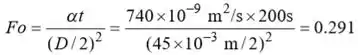
Desde , o termo único de aproximação é válido. Da Tabela 5.1 com . Portanto,
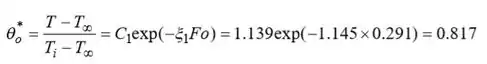
Logo,
