Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 5.Problemas - Ex. 110
Seja a parede composta do Problema 2.53. Na parte (d),foi solicitado a você fazer um esboço dos históricos das temperaturas em x = 0 e L durante o período transiente entre os casos 2 e 3. Calcule e represente esses históricos usando um método de elementos finitos, um método de diferenças finitas (com Ax = 5 mm e A/ = 1,2 s) e/ou um procedimento alternativo de sua escolha. Se você usar mais de um método, compare os respectivos resultados.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! O que sabemos das condições iniciais?
Aquecedor elétrico colocado entre duas placas grossas cujas superfícies sofrem convecção. O caso 2 corresponde à operação em estado estacionário com perda de refrigerante na superfície x = -L. De repente, ocorre uma segunda condição de perda de refrigerante na superfície x = +L, mas o aquecedor permanece energizado pelos próximos 15 minutos. O caso 3 corresponde à eventual condição de estado estacionário após o segundo evento de perda de refrigerante.
A distribuição de temperatura para o Caso 2 mostrada no gráfico acima representa a condição inicial para o período de tempo após o segundo evento de perda de refrigerante. As condições de contorno em x = ±L são adiabáticas e o fluxo do aquecedor é mantido em
para
Usando FEHT, o aquecedor é representado como uma placa de espessura Lh = 0,5 mm com capacitância térmica muito baixa (ρ = 1 kg/m e c = 1 J/kg⋅K), condutividade térmica muito alta (k= 10.000 W/m ⋅K), e uma taxa de geração volumétrica uniforme de
para
Na caixa Especificar | Caixa de geração, a geração foi prescrita pelo arquivo de pesquisa (consulte a Ajuda do FEHT): ‘hfvst’,1,2,Time. Este arquivo do bloco de notas é composto por quatro linhas, com os valores em cada linha separados por um único espaço de tabulação:
Passo 2
As histórias de temperatura-tempo são mostradas no gráfico abaixo para as superfícies x = - L (curva mais baixa, 13) ex = +L (19) e o ponto central x = 0 (curva mais alta, 14). O ponto central experimenta a temperatura máxima de 89°C no momento em que o aquecedor é desativado, t = 900 s.
Passo 3
Para o método de solução de diferenças finitas, o arranjo nodal para o sistema é mostrado abaixo.
O construtor de modelo IHT Ferramentas | Equações de diferenças finitas | Unidimensional pode ser usado para obter os FDEs para os nós internos (02-04, 07-10) e os nós de contorno adiabáticos (01, 11).
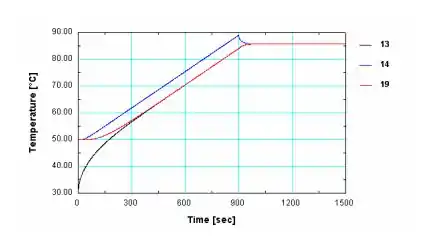
Comparando chegamos a duas conclusões:
(1) A temperatura máxima durante o período transiente está no ponto central e ocorre no instante em que o aquecedor é desativado, T(0, 900s) = 89°C. Após 300 s, observe que as duas temperaturas de superfície são quase as mesmas e nunca sobem acima da temperatura final do estado estacionário.
(2) Ambos os métodos de solução FEHT e IHT fornecem resultados idênticos. Suas soluções de estado estacionário concordam com o resultado de um balanço de energia em uma base de intervalo de tempo produzindo Tss = 86,1°C.