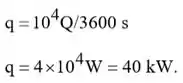Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 74
Bilhas de aço inoxidável (AISI 304), que foram aquecidas uniformemente até 850°C, são endurecidas pelo resfriamento em um banho de óleo mantido a 40°C. O diâmetro de cada esfera é de 20 mm e o coeficiente convectivo associado ao banho de óleo é de
(a) Se o resfriamento deve prosseguir até que a temperatura superficial das esferas atinja , quanto tempo as esferas devem permanecer imersas no banho de óleo? Qual é a temperatura no centro das esferas no instante da conclusão do período de resfriamento?
(b) Se 10.000 bilhas devem ser resfriadas a cada hora, qual é a taxa na qual energia deve ser removida pelo sistema de resfriamento do banho de óleo de modo a mantê-lo à temperatura de 40°C?
Passo 1
Vamo lá galera! (a) Para determinar se o uso do método de capacidade por blocos é adequado, primeiro calcule,
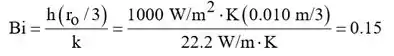
Concluímos que, embora o método da capacitância por blocos possa ser usado como primeira aproximação, a solução exata deve ser usada no interesse de melhorar a precisão. Assumimos que a aproximação a um prazo é válida e verificamos mais tarde. Portanto, com
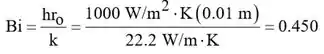
Da tabela 5.1,
E a eq. 5.53b pode ser resolvida para,
Passo 2
Então a Equação 5.53c pode ser resolvida para :
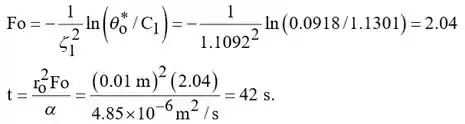
Note que a aproximação a um prazo é precisa, uma vez que Fo > 0,2. Também:
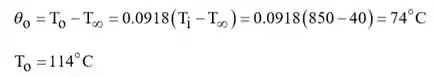
Passo 3
(b) A equação 5,55 pode ser usada para calcular a perda de calor de uma única bola:
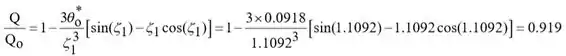
Portanto, da equação 5.47,
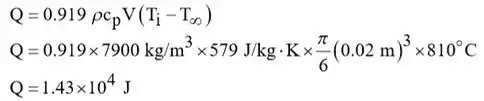
é a quantidade de energia transferida de uma única bola durante o processo de resfriamento. Portanto, a taxa de resfriamento do banho de óleo deve ser,
