Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 53
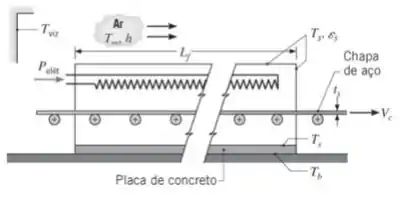
Em um estágio de um processo de têmpera, a temperatura de uma chapa de aço inoxidável AISI 304 é levada de para ao passar através de um forno aquecido eletricamente a uma velocidade de . A espessura e largura da chapa são e , respectivamente, enquanto a altura, a largura e o comprimento do forno são , e , respectivamente. O teto e as quatro paredes laterais do forno estão expostos ao ar ambiente e a uma grande vizinhança, ambos a . Sua temperatura superficial, coeficiente de transferência de calor por convecção e emissividade correspondentes são , e . A superfície inferior do forno também se encontra a e pousa sobre uma placa de concreto com de espessura, cuja base encontra-se a . Estime a potência elétrica que deve ser fornecida ao forno.
Passo 1
Começamos o problema calculando a temperatura média da chapa de aço inoxidável AISI 304:
Sendo:
;
.
Temos:
Agora, temos que obter as propriedades do aço inoxidável AISI 304 na Tabela A.1: ‘’Propriedades termofísicas de sólidos metálicos selecionados’’ sob a temperatura de :
O calor específico deve ser calculado por interpolação entre e :
Pela Tabela A.3: “Propriedades termofísicas de materiais comuns” obteremos o valor da condutividade térmica do concreto sob a temperatura de :
Passo 2
Analisando o balanço de energia, temos:
Não é pouca variável não hein....
Para facilitar, coloque-as dispostas!Dados:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Temos: