Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 86
Como está evidente nos dados de propriedades nas Tabelas A.3 e A.4, a condutividade térmica do vidro na temperatura ambiente é mais do que 50 vezes maior do que a do ar. Consequentemente, é desejável que se use janelas de vidro duplo, nas quais as duas lâminas de vidro delimitam um espaço de ar. Se a transferência de calor através do espaço de ar for por condução, a resistência térmica correspondente pode ser aumentada pelo aumento da espessura L do espaço. Entretanto, há limites para a eficácia desta proposta, pois correntes de convecção são induzidas se L for superior a um valor crítico, além do qual a resistência térmica diminui.
Considere ar atmosférico confinado por lâminas verticais nas temperaturas de T1 = 22°C e T2 = –20°C. Sendo o número de Rayleigh crítico para o início da convecção igual a RaL ≈ 2000, qual é o espaçamento máximo permitido para a condução através do ar? Como esse espaçamento é afetado pelas temperaturas das lâminas? Como ele é afetado pela pressão do ar, como, por exemplo, pela adoção de uma pressão inferior à atmosférica (vácuo) no espaço?
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos uma janela dupla de vidro com um espaço de ar entre as duas lâminas da janela a diferentes temperaturas, como mostra o esquema ilustrativo abaixo:
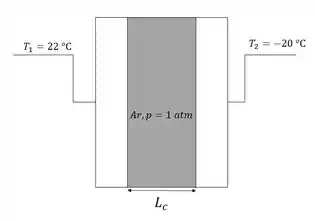
Para resolver essa questão, devemos calcular a espessura crítica para a qual o número de Rayleigh será , fazendo com que se inicie a convecção natural e haja mais um mecanismo de transferência de calor no processo.
O número de Rayleigh crítico para uma placa plana é:
Sendo o comprimento crítico que queremos calcular, a aceleração da gravidade, o coeficiente de expansão térmica do ar, a viscosidade cinemática do ar e a difusividade térmica do ar.
Pra resolver a questão vamo precisar buscar as propriedades do ar a 1 atm na Tabela A.4 (página 634) a uma temperatura média entre de :
Pronto, agora podemos resolver a questão no próximo passo.
Passo 2
Pra finalizar a questão, vamos substituir as propriedades que buscamos na equação que eu te mostrei no passo anterior e calcular o espaçamento crítico entre as lâminas da janela:
Além disso, a questão pede que a gente avalie como esse espaçamento é afetado pelas temperaturas das lâminas e pela pressão do ar.
Bem, a diferença de temperaturas está no denominar da equação que eu te mostrei nesse passo, fazendo com que aumente com a diminuição dessa diferença.
A viscosidade cinemática e a difusividade térmica podem ser calculadas a partir das seguintes equações:
Como, para um gás ideal, depende diretamente da pressão, e diminuem com o aumento de pressão. Como essas duas propriedades estão no numerador da equação lá em cima, isso significa que também diminui com o aumento da pressão.
Pronto, matamos a questão junto ;)
Resposta
O espaçamento crítico entre as lâminas da janela é .