Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 76
Considere dois cilindros horizontais concêntricos de diâmetros e e de comprimento. As superfícies interna e externa dos cilindros são mantidas a e , respectivamente. Determine a taxa de transferência de calor por convecção natural entre os cilindros se o espaço anular for preenchido com (a) água e (b) ar.
Passo 1
O diâmetro do cilindro interno:
O diâmetro do cilindro externo:
Comprimento dos cilindros:
Temperatura da superfície do cilindro interno:
Temperatura da superfície do cilindro externo:
Premissas:
1) Existem condições operacionais estáveis.
2) O ar é um gás ideal com propriedades constantes.
3) A pressão do ar no gabinete é de 1 atm.
4) A transferência de calor por radiação é insignificante.
Passo 2
Podemos fazer o seguinte esquema para demostras o que esta sendo pedido.
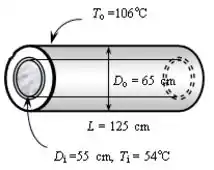
Passo 3
a) Queremos determinar a taxa de transferência de calor do cilindro externo para o cilindro interno por convecção natural quando o fluido entre eles é água.
Para isso, podemos começar calculando a temperatura média da seguinte maneira:
Vamos calcular também o comprimento característico. Podemos usar a seguinte relação:
Passo 4
Com a temperatura média, podemos obter as propriedades da água que preenche o espaço anular:
Condutividade térmica:
Densidade:
Viscosidade dinâmica:
Número Prandtl:
Coeficiente de expansão volumétrica:
A viscosidade cinemática é dada por:
Passo 5
Com os dados obtidos, nós vamos calcular agora o número de Rayleigh usando a seguinte expressão:
Aqui, é o número de Rayleigh, é a aceleração devido à gravidade, é a viscosidade cinemática e é o comprimento característico. Substituindo os termos da equação pelos dados coletados, temos:
Vamos calcular também o fator geométrico da seguinte maneira:
Aqui, e são os diâmetros dos cilindros e é o comprimento característico. Substituindo os termos da equação pelos dados coletados, temos:
Passo 6
Com os dados obtidos acima, podemos calcular a condutividade térmica efetiva usando a seguinte relação:
Substituindo os termos da equação pelos dados calculados anteriormente, temos:
Passo 7
Assim, temos que a taxa de transferência de calor entre os cilindros quando o fluido é água é a seguinte:
Substituindo os termos da equação pelos dados calculados anteriormente, temos:
Portanto, a taxa de transferência de calor quando o fluido é água é .
Passo 8
b) Com a temperatura média de , podemos obter as propriedades do ar na pressão de que preenche o espaço anular:
Condutividade térmica:
Viscosidade cinemática:
Número Prandtl:
O coeficiente de expansão de volume é dado por:
Onde é a temperatura de filme, que neste caso é a mesma que a temperatura média, em kelvin.
Passo 9
Com os dados obtidos, nós vamos calcular agora o número de Rayleigh usando a seguinte expressão:
Substituindo os termos da equação pelos dados coletados, temos:
Vamos calcular também o fator geométrico da seguinte maneira:
Substituindo os termos da equação pelos dados coletados, temos:
Passo 10
Com os dados obtidos acima, podemos calcular a condutividade térmica efetiva usando a seguinte relação:
Substituindo os termos da equação pelos dados calculados anteriormente, temos:
Passo 11
Assim, temos que a taxa de transferência de calor entre os cilindros quando o fluido é ar é a seguinte:
Substituindo os termos da equação pelos dados calculados anteriormente, temos:
Portanto, a taxa de transferência de calor quando o fluido é ar é .
Resposta
a)
b)