Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 7.Problemas - Ex. 97
Explore a variação na velocidade de propagação de ondas dada pela equação do Problema 7.1 para um escoamento de água de superfície livre. Determine a profundidade de operação para minimizar a velocidade de ondas capilares (ondas de pequeno comprimento de onda, também chamadas de ondulações). Inicialmente, considere que o comprimento de onda é muito menor que a profundidade da água. Em seguida, explore o efeito da profundidade. Que profundidade você recomenda para uma mesa d’água de visualização do fenômeno de ondas em escoamento compressível? Qual é o efeito da redução da tensão superficial pela adição de um detergente?
Passo 1
Beleza, a primeira coisa que devemos fazer é pegar a equação apresentada no Problema 7.1, então, teremos:
Então, nesse caso temos como velocidade da onda, como tensão superficial, como densidade do fluido, sendo o comprimento de onda, a aceleração da gravidade e a profundidade de operação.
Passo 2
Agora, analisando a equação apresentada no passo 1, temos que o termo:
Leva em consideração a tensão superficial e nos fornece uma velocidade que é inversamente proporcional ao comprimento de onda e diretamente proporcional à tensão superficial, então, ele será relevante (grande) quando tivermos pequenos comprimentos de onda. Agora, já o segundo termo:
Por sua vez leva em consideração a gravidade e é diretamente proporcional ao comprimento de onda, de modo que ele só sera relevante para grandes comprimentos de onda. Agora, já a tangente hiperbólica:
É proporcional à profundidade e inversamente proporcional ao comprimento de onda. Então, para pequenos valores de comprimento de onda, o argumento da tangente hiperbólica tende ao infinito e a tangente hiperbólica em si tende a 1.
Passo 3
Então, ilustrando o comportamento da curva da equação do passo 1, com comportamento e características descritas no passo 2, temos:
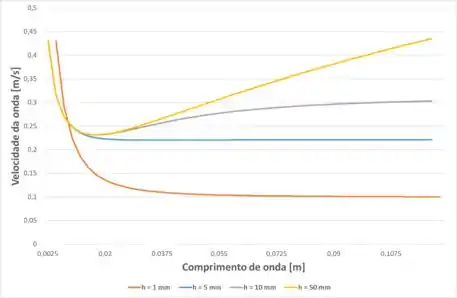
Resposta
Ei, a resposta está no passo a passo :)