Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 81

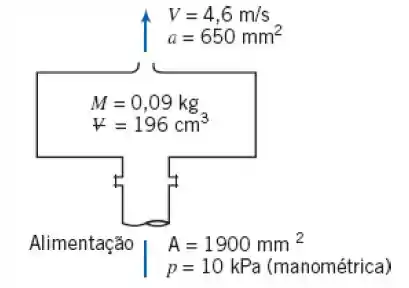
4.81 Um dispositivo de formação de jato é mostrado no diagrama. A água é fornecida a p=10 kPa (manométrica) através da abertura flageada da água 1900 mm². A água sai do dispsitivo em um jato livre, em regime permanente, à pressão atmosférica. A área e a velocidade do jato são a=650 mm² e V=4,6 m/s. O dispositivo tem massa de 0,09 kg e contém V = 196   c m 3 de água. Determine a força exercida pelo dispositivo sobre o tubo de suprimento de água.

Passo 1

Aqui vamos usar somente a componente y da equação de momento:

F R y + F B y = ∂ ∂ t ∫ V C v ρ   d V + ∫ C V v ρ V → d A →                           i

Como é regime permantente, então:

∂ ∂ t ∫ V C v ρ   d V = 0                     i i

Da equação da continuidade, chamada carinhosamente de conservação de massa, para acharmos a velocidade de entrada, v 1 , que não é dada no enunciado:

v 1 ρ A 1 = v 2 ρ A 2

Como v 2 = V , A 1 = A , A 2 = a e o escoamento é incompressível ( ρ = c t e ) ,

v 1 A = V a

v 1 = V a A

Achando F B y (que são o peso do dispositivo e da água contida nele)

F B y = - M g - ρ V g                         i i i

Achando ∫ C V v ρ V → d A →

  ∫ C V v ρ V → d A → = v 1 - ρ v 1 A 1 + v 2 ρ v 2 A 2

ATENÇÃÃÃÃÃO:

Aparece um sinal negativo na frente do “ ρ v 1 A 1 " resumidamente porque o vetor velocidade está no sentido contrário ao vetor normal à area (o que não acontece com v 2 e A 2 , pois o vetor velocidade e o vetor normal à area estão no mesmo sentido.

Continuando e substituindo

∫ C V v ρ V → d A → = v 1 - ρ v 1 A 1 + v 2 ρ v 2 A 2

∫ C V v ρ V → d A → = V a A - ρ V a A A + V ρ V a

∫ C V v ρ V → d A → = - ρ V 2 a a A - 1

∫ C V v ρ V → d A → = ρ V 2 a 1 - a A                       i v

Passo 2

Substituindo i i ,   i i i e ( i v ) em i

F R y - M g - ρ V g   = 0 +   ρ V 2 a 1 - a A

R y + p 1 A - M g - ρ V g = ρ V 2 a 1 - a A

Substituindo os valores (considerango g = 9,81   m / s 2 e vamos passar logo as unidades das áreas para m² para não nos esrolarmos e acabar errando besteira... A = 1900   m m 2 = 0,0019   m 2 , a = 650   m m 2 = 0,00065   m 2 , ρ = 999   k g / m 3 , p 1 = 10   k P a   , V = 4,6   m / s , g = 9,81   m / s 2 , M = 0,09   k g e V = 196   c m 3 = 0,000196   m 3

Logo

R y = - p 1 A + M g + ρ V g + ρ V 2 a 1 - a A

R y = - 10000 0,0019 + 0,09 9,81 + 999 4,6 2 0,00065 1 - 0,00065 0,0019   + 999 0,000196 9,81

R y = - 19 + 0.8829 + 9,03 + 1,92084

R y = - 7,16   N

F y = - R y = 7 , 16   N

Resposta

F y = R y = 7,16   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.96 Água é descarregada a vazão de 0,3 m³/s por uma fenda estreita em um tubo de 200 mm de diâmetro. O jato resultante, horizontal e bidimensional, tem 1 m de comprimento e espessura de 20 mm, mas co
4.101 Um fluido incompressível escoa em regime permanente na região de entrada de um canal bidimensional de altura 2 h = 100m m e largua w = 25m m . A vazão é Q = 0,025m ³ / s ³ . Encontre a velocidad
4.102 Um fluido incompressível escoa em regime permanente na região de entrada de um tubo circular de raio R = 75m m . A vazão é Q = 0,1m ³ / s ³ . Encontre a velocidade unifrome U 1 na entrada. A dis
4.97 Água escoa em regime permanente através da curva de 90° do Problema 4.39. O escoamento na entrada está a p 1 = 185k P a (absoluta). O escoamento na saída é não uniforme, vertical e à pressão atmo
4.99 Um pequeno objeto redondo é testado em um túnel de vento de 0,75 m de diâmetro. A pressão é uniforme nas seções 1 e 2. A pressão a montante é 30 mm de H 2 O (manométrica), a pressão a jusante é 1