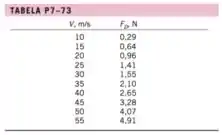
Um modelo em escala para de um novo automóvel esporte é testado em um túnel de vento. O automóvel protótipo tem de comprimento, de altura e de largura. Durante os testes, a velocidade da esteira de solo móvel é ajustada para que sempre coincida com a velocidade do ar que se move através da seção de teste. A força de arrasto aerodinâmico , é medida como função da velocidade do túnel de vento; os resultados experimentais estão listados na Tabela . Trace o coeficiente de arrasto como função do número de Reynolds , onde a área usada para o cálculo de é a área frontal do automóvel modelo (considere ), e a escala de comprimento usada para o cálculo do é a largura do automóvel . Atingimos a semelhança dinâmica? Atingimos a independência do número de Reynolds em nosso teste no túnel de vento? Estime a força de arrasto aerodinâmico sobre o automóvel protótipo que se move na rodovia a (). Considere que o ar do túnel de vento e o ar que escoa sobre o automóvel protótipo estão a e a pressão atmosférica.

Para a última velocidade da tabela (a qual obedece a escala ), temos o seguinte valor de coeficiente de arrasto e numero de Reynolds:

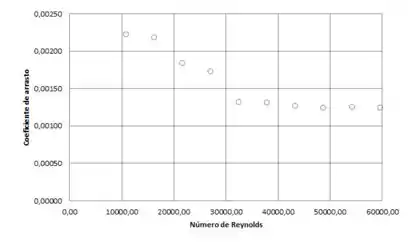
Aos outros valores, segue-se o mesmo procedimento. Para facilitar nossa vida, vamos utilizar o Excel e plotarmos o gráfico com os valores:

Calculamos agora o numero de Reynolds para o automóvel protótipo, para determinarmos a semelhança.

Assim, a semelhança geométrica entre o protótipo e o modelo foi alcançado, mas a semelhança dinâmica não, uma vez que o protótipo é sete vezes maior que o modelo.

Quanto a possibilidade de atingirmos a independência do número de Reynolds, atingimos sim, uma vez que para temos um coeficiente de arrasto que se estabilizou a .

Calculando a força de arrasto aerodinâmico sobre o automóvel protótipo, temos:

Prontinho!!