Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 98

Como uma extensão do Exemplo 3.10, considere a placa e o carrinho (ver Figura 3.10a) desimpedidos horizontalmente, com rodas sem atrito. Deduza (a) a equação do movimento para a velocidade do carrinho V c t   e (b) a fórmula para o tempo requerido para o carrinho se acelerar do repouso até 90% da velocidade do jato (supondo que o jato continua a atingir a placa horizontalmente). (c) Calcule valores numéricos para a parte (b) usando as condições do Exemplo 3.10 e um carrinho de massa 2kg.

Passo 1

Bora lá!

Vamos ter o seguinte esquema:

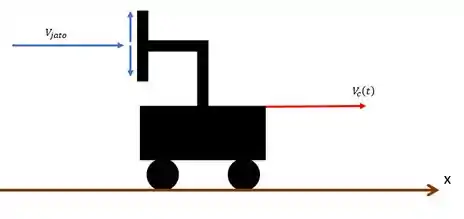
Beleza! Para a letra (a) vamo utilizar a equação 3.49 com a a r e l a t i v a = a c a r r o e ∑ F x = 0 , assim:

∑ F x - a r e l a t i v a , x m = ∫ u ρ V ⋅ n d A = - m c a r r o d V c d t = - ρ j a t o A j a t o V j a t o - V c 2

Passo 2

Pela equação encontrada em (a), podemos tirar um EDO de primeira ordem que pode ser resolvida por separação de variáveis, assim:

∫ 0 V c d V c V j a t o - V c 2 = ρ j a t o A j a t o m c a r r o ∫ 0 t d t

Resolvendo,

V c V j a t o = V j a t o ρ j a t o A j a t o m c a r r o t 1 + V j a t o ρ j a t o A j a t o m c a r r o t = 0,90

Daí, pra (b), teremos:

t 90 % = 9 ρ j a t o A j a t o m c a r r o V j a t o = 9 m c a r r o ρ j a t o A j a t o V j a t o

Passo 3

Para (c) temos os seguintes dados, m c a r r o = 2 k g ,   ρ j a t o = 1000   k g / m 3 ,   A j a t o = 0,0003   m 2 ,   V j a t o = 20   m / s , substituindo na equação encontrada em (b), teremos:

t 90 % = 9 2   k g 1000 k g m 3 0,0003   m 2 20 m s = 3   s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No escoamento laminar de um fluido em condutos circulares, o diagrama de velocidades é representado pela equação v = v m a x 1 - r R 2 , onde v m a x é a velocidade no eixo do conduto, R é o raio do c
No tubo da figura, determinar a vazão em volume, em massa, em peso e a velocidade média na seção 2 , sabendo que o fluido é água e que A 1 = 10c m 2 e A 2 = 5c m 2 . ( ρ H 2 O = 1000k g / m 3 , g = 10
Um gás ( γ = 5N / m 3 ) escoa em regime permanente com uma vazão de 5k g / s pela seção A de um conduto retangular de seção constante de 0,5m por 1m . Em uma seção B , o peso específico do gás é 10N /
A água escoa por um conduto que possui dois ramais em derivação. O diâmetro do conduto principal é 15c m e os das derivações são 2,5c m e 5c m , respectivamente. O perfil das velocidades no conduto pr
Um propulsor a jato queima 1k g / s de combustível quando o avião voa à velocidade de 200m / s . Sendo dados ρ a r = 1,2k g / m 3 , ρ g = 0,5k g / m 3 (na seção 2 ), A 1 = 0,3m 2 e A 2 = 0,2m 2 , dete