Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 17

Um propulsor a jato queima 1   k g / s de combustível quando o avião voa à velocidade de 200   m / s . Sendo dados ρ a r = 1,2   k g / m 3 , ρ g = 0,5   k g / m 3 (na seção 2 ), A 1 = 0,3   m 2 e A 2 = 0,2   m 2 , determinar a velocidade dos vages v g na seção de saída.

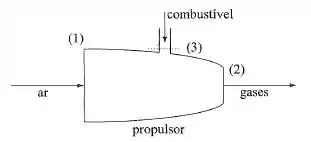
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para esta questão vamos aplicar a equação da continuidade que diz que a vazão mássica que entra deve ser igual a que sai, temos que:

Q m a r + Q m c o m b = Q m g a s e s

Desenvolvendo, temos que:

ρ a r v a r A a r + Q m c o m b = ρ g a s e s v g a s e s A g a s e s

Substituindo pelos respectivos valores, temos que:

1,2 ⋅ 200 ⋅ 0,3 + 1 = 0,5 ⋅ v g a s e s ⋅ 0,2

v g a s e s = 730   m / s

Resposta

v g a s e s = 730   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mangueira de incêndio tem um diâmetro interno de 125 m m e água está escoando a 2,271 m 3 / m i n . O escoamento sai através de um bocal com um diâmetro D n . Para escoamento permanente, qual deve
Três tubos forncecem água em regime permanente a 20 ° C para um tubo maior de saída mostrado na figura P3.8. A velocidade V 2 = 5 m / s e a vazão de saída Q 4 = 120 m 3 / h . Encontre: V 1 ; V 3 ; V 4
Um tanque esférico, com diâmetro de 35c m , está perdendo ar através de um furo de 5m m de diâmetro na sua lateral. O ar sai pelo furo a 360m / s com massa específica de 2,5k g / m 3 . Supondo uma mis
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na Figura P 3.6 , uma aproximação para a distribuição de velocidade na saída é u ≈ 2 g h - z 1 2 , onde h é a profund
Estenda o Problema P3.92 para incluir o atrito na parede devido a uma tensão de cisalhamento média linear (laminar) na forma τ ≈ c V , em que c é uma constante. Encontre a equação diferencial para dV/