Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 117

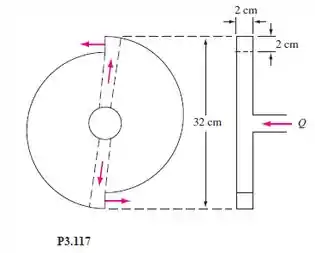
Uma turbomáquina simples é constituída de um disco com dois dutos internos que saem tangencialmente através de seções quadradas, como na Figura P3.117. Água a 20°C entra perpendicularmente ao disco no centro como mostra a figura. O disco deve acionar, a 250 rpm, um pequeno dispositivo cujo torque resistente é 1,5 N.m. Qual é o fluxo de massa adequado, em kg/s.

Passo 1

Alô você! Simbora!

Contar um segredo pra você, essa questão é uma versão meio alterada do exemplo 3.15 do livro, da uma olhadinha lá que vamos usar umas coisinhas!

Na nossa questão, temos uma velocidade de torração constante, tendo em mente um retardo pelo torque, isso pode ser dado pela seguinte equação (do exemplo 3.15):

Passo 2

Galera, daí já conseguimos encontrar a velocidade de saída da água, porém para a vazão nos dois braços, ou seja, nas duas saídas, teremos:

Esse, se refere a área da saída para entrar no nosso disco.

Substituindo na nossa equação e colocando os valores:

Resolvendo, chegaremos a:

Passo 3

Para encontrar o fluxo mássico, basta fazer:

Substituindo,

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4.89 A figura mostra um redutor em uma tubulação. O volume interno do redutor é 0,2 m³ e a sua massa é 25 kg. Avalie a força total de reação que deve ser feita pelos tubos adjacentes para suportar o r

4.83 O bocal mostrado descarrega uma cortina de água por meio de um arco de 180°. A uma distância radia de 0,3 m a partir da linha de centro do tubo de suprimento, a velocidade da água é 15 m/s e a es

4.85 Uma máquina típica para testes de motores a jato é mostrada na figura, juntamente com alguns dados de testes. O combustível entra verticalmente no topo da máquina a uma taxa igual a 2% da vazão e

4.86 Considere o escoamento através da expansão súbita mostrada. Se o escoamento for incompressível e o atrito desprezível, mostre que o aumento de pressão, Δ p = p 2 - p 1 , é dado por Δ p 1 2 ρ V -

4.93 Considere o escoamento permanente e adiabático de ar através de um longo tubo retilíneo com área de seçao transversal de 0,05 m². Na entrada do tubo, o ar está a 200 kPa (manométrica), 60°C e tem