Fala-se que o novo paraquedas pessoal ATPS, do Exército norte-americano, é capaz de trazer ao solo uma carga de 1780 N, soldado mais mochila, a 4,8 m/s em Denver, Colorado (a 1609 m de altitude). Se considerarmos que a tabela 7.3 seja válida, qual será o diâmetro aproximado desse novo paraquedas?

E aí, gente!!! Tudo bem? Bora dar uma encarada nesse exercício?

Primeiro, vamos desenhar e observar que a força peso e a força de arrasto são as forças que estão ali atuando. Vamos desprezar os efeitos de aceleração, beleza?

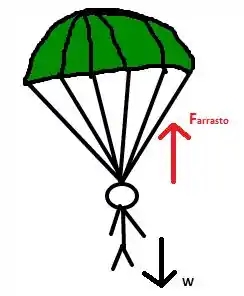
Com isso, temos que

Baseado na tabela 7,3 temos que e na altitude que Denver estar a mais ou menos 1600 m de altitude, o que faz com que a densidade do ar, de acordo com a tabela A-6 do livro, ser igual a aproximadamente