Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 21
Feixes de laser são usados para processar termicamente materiais em uma ampla gama de aplicações. Frequentemente, o feixe é deslocado ao longo da superfície do material segundo um padrão desejado. Seja o processo de aquecimento a laser do Problema 4.18, exceto agora pelo fato de que o feixe de laser se desloca pela superfície do material a uma velocidade U. Uma temperatura superficial adimensional máxima pode ser bem correlacionada por uma expressão na forma [Nissin, Y. I., A. Lietoila, R. G. Gold e J. F. Gibbons, J. Appl. Phys., 51, 274, 1980]:
na faixa, sendo a velocidade adimensional, conhecida como o número de Peclet. Para esse problema, sendo α a difusividade térmica do material. A temperatura máxima no material não ocorre diretamente abaixo do feixe de laser, mas em uma distância de retardo, , atrás do centro do feixe em deslocamento. A distância de retardo adimensional pode ser correlacionada com por [Sheng, I. C. e Y. Chen, J. Thermal Stresses, 14, 129, 1991]:
(a) Para o tamanho e forma do feixe de laser e para o material do Problema 4.18, determine a potência do laser requerida para se obter para . A massa específica e o calor específico do material são e respectivamente.
(b) Determine a distância de retardo, , associada a .
(c) Represente graficamente a potência do laser necessária para atingir para
Passo 1
Bora para mais uma questão?! Aqui nós temos a relação entre a temperatura máxima do material e sua localização e as velocidades de varredura.
Com isso queremos encontrar a potência necessária do laser para atingir a temperatura operacional desejada para determinado material o tamanho e a velocidade do feixe. Além da distância do retardo que separa o centro do feixe e a localização da temperatura máxima.
Por fim, queremos fazer a plotagem da potência necessária do laser para velocidades na faixa de. Show?! Então vamos lá!
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições em estado estacionário;
(2) Propriedades constantes;
(3) Meio semi-infinito;
(4) Perda insignificante de calor da superfície superior.
Temos que a difusividade térmica dos materiais é,
E o número do peclet é,
Passo 3
Como o valor do número Peclet está dentro da faixa de correlação fornecida na declaração do problema, a temperatura máxima correspondente a um feixe estacionário que fornece a mesma potência vai ser,
Substituindo os valores,
Com o símbolo agora representando a absorção, uma vez que é usado para difusividade térmica, vamos ter:
Substituindo os valores,
Passo 4
Para a distância do atraso nós vamos usar a seguinte expressão,
Substituindo os valores,
Por fim, vamos fazer o gráfico da potência necessária do laser versus a velocidade de varredura que vai ficar com a seguinte carinha:
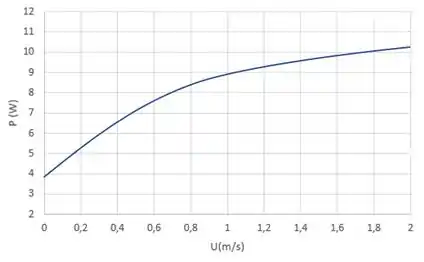
Resposta
