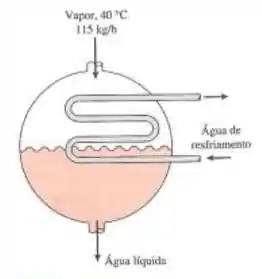
Vapor sai a 40°C da turbina de uma central elétrica a vapor para ser condensado em um grande condensador por água de resfriamento fluindo através dos tubos de cobre de diâmetro interno de 1 cm e 1,5 cm de diâmetro externo, a uma temperatura média de 20°C. O calor de condensação da água a 40°C é de . Os coeficientes de transferência de calor são no lado do vapor e no lado da água. Determine o comprimento do tubo necessário para condensar o vapor a uma taxa de
Passo 1
Então galerinha, preparados??
O que temos aqui?
Nós temos um tubo, sem isolamento, contendo vapor no seu exterior e um ambiente interno contendo água.
Então teremos apenas três resistências, bora desenhar?
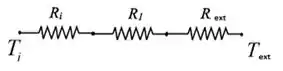
Então:
Agora que já sabemos como calcular cada uma nós só precisamos saber as áreas, certo?
Bora lá?
Passo 2
Para calcular a área nós vamos usar o comprimento equivalente a 1 m e depois vamos comparar o valor obtido aqui com o calor total, ok?
A área interna da seção transversal é dada por:
Para a área externa nós levamos em consideração o diâmetro externo do tubo:
Beleza !! Próximo passo?
Passo 3
Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências:
Sabendo que podemos adaptar as resistências:
Substituindo:
Como estão todas em série, a resistência total é dada por:
Passo 4
Agora sim nós conseguimos saber qual será a perda de calor para o ambiente.
Usamos a fórmula do calor:
Substituindo:
Como a variação em graus Celsius e kelvin é a mesma:
Então, em 1 metro de tubo de cobre ocorre a troca de 125,26 W de calor, tranquilo?
Então:
Agora vamos guardar esta informação!!
Passo 5
Legal ! Já sabemos quanto calor é trocado por metro e agora vamos achar a troca total de calor que ocorre, ok?
Para isso nós vamos usar a taxa de calor necessário para condensar o vapor.
Se não se lembram da fórmula não tem problema! Lá vai ela:
Pelo problema sabemos que:
Substituindo:
Em W:
Agora que sabemos disso podemos achar o comprimento simplesmente dividindo o calor total pelo calor por metro de tubo:
Substituímos:
E é isso aí, galera !!