Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 73
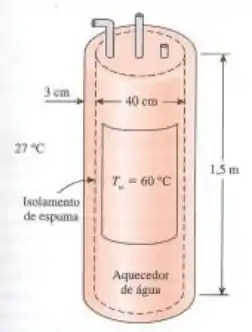
Considere um aquecedor elétrico de água quente com 1,5 m de altura e 40 cm de diâmetro e mantenha a água quente a 60°C. O reservatório está localizado em uma pequena sala cuja temperatura média é de 27°C e os coeficientes de transferência de calor nas superfícies interna e externa do aquecedor são de , respectivamente. O reservatório é colocado em outro tanque de chapa de metal de 46 cm de diâmetro, de espessura desprezível, e o espaço entre os dois tanques é preenchido com isolamento de espuma . As resistências térmicas do tanque de água e da fina casca externa de folha de metal são muito pequenas e podem ser negligenciadas. O preço da eletricidade é de e o proprietário da casa paga pelo aquecimento da água. Determine a fração do custo da energia da água quente para o dono da casa devido à perda de calor do tanque.
Conjuntos de isolamento de reservatórios de água quente constituídos de isolante de fibra de vidro de 3 cm de espessura, grande o suficiente para envolver todo o tanque, estão disponíveis no mercado por cerca de . Se esse isolamento for instalado neste reservatório de água pelo próprio proprietário da casa, quanto tempo levará para que esse isolamento adicional se pague?
Passo 1
Shoow!!
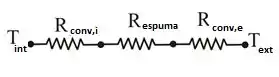
Vamos começar como de costume, desenhando as queridas resistências. Na parte interna contendo a água quente existe uma resistência convectiva interna, temos a resistência oferecida pela espuma e finalizamos com a resistência convectiva externa:
Então:
Já sabemos como calcular as resistências, só precisamos das áreas.
Bora lá?
A área interna da seção transversal é dada por:
Para a área externa nós levamos em consideração o diâmetro interno mais o comprimento da espuma:
Então:
Passo 2
Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências:
Sabendo que podemos adaptar a resistência para a espuma:
Substituindo:
Como estão todas em série, a resistência total é dada por:
Lembrando da fórmula do calor:
E substituindo:
Como a variação em graus Celsius e kelvin é a mesma:
Beleza! Achamos que o trocador de calor perde cercar de
Passo 3
Para responder o custo anual deste calor perdido, vamos precisar achar inicialmente a quantidade de calor desperdiçada ao longo desse um ano.
Para isso vamos multiplicar a taxa de calor obtida anteriormente pelo tempo, em horas:
Usamos a fórmula:
E transformando W em kW
Se sabemos que o custo é dado por
Se ele paga por ano a fração de energia desperdiçada será:
Sendo assim, 15,2% do que ele paga por ano é devido ao calor que é perdido!
Passo 4
Beleza galera! Agora temos uma resistência a mais
Se adicionamos mais uma camada de isolante iremos variar a área externa, mas a interna permanece igual:
Para a área externa nós levamos em consideração o diâmetro anterior mais o comprimento do isolamento extra:
Então:
Vamos guardar esta informação e olhar para as resistências!
As resistências interna e da espuma não variam:
A resistência externa agora leva em conta a nova área:
E para o isolamento extra
Substituindo:
Como estão todas em série, a resistência total é dada por:
E agora vamos colocar na fórmula:
Passo 5
Já descobrimos que ao invés de perder agora o dono da casa perderá somente
Qual a economia??
Bom galera, sabemos que o custo deste isolamento será dado por:
Substituiremos nossos dados para descobrir esta variação de tempo:
Vamos transformar em meses:
E fiiim !!
Resposta
Fração do Custo de Calor Perdido: ;
Tempo para que o isolante se pague: