Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 56

In Fig. P2.55, gate AB is 5 ft wide into the paper, and stop

B will break if the water force on it equals 9200 lbf. For

what water depth h is this condition reached?

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Considerando o diagrama que indica as dimensões

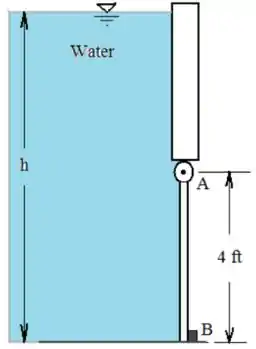
Passo 2

Calcule a distância centroidal da superfície da água.

h ‾ = ( h - 4 ) + C G

Aqui, o centro de gravidade do portão retangular é CG. Substitua 2 f t para C G .

h ‾ = ( h - 4 ) + 2   = ( h - 2 ) f t

Calcule a área do portão retangular.

A = 5 × 4   = 20 f t 2

Calcule a força hidrostática total no portão.

F = γ á gua   A h ‾

Aqui, γ á gua   está o peso específico. Substitua 20 f t 2 por A , e ( h - 2 ) f t por h ‾ .

F = 62.4 × 20 × ( h - 2 )   = 1248 ( h - 2 ) l b f

Passo 3

Calcule o Momento de inércia do portão.

I G = b × h 3 12

Substitua 5 f t para b .

I G = 5 × 4 3 12   = 26.66

Passo 4

Calcular o centro de pressão a partir da superfície livre da água.

h * = I G A h ‾ + h ‾   = 26.66 20 × ( h - 2 ) + ( h - 2 )

Calcule a distância de A até a linha de ação da pressão.

A C = 2 f t + h * - h -

Substitua 26.66 20 × ( h - 2 ) + ( h - 2 ) para h * , e ( h - 2 ) f t por h ‾

A C = 2 + 26.66 20 × h - 2

Passo 5

Considerando o seguinte diagrama de corpo livre para o portão com as reações

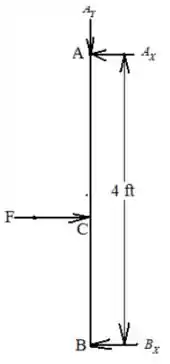
Passo 6

Considerando o momento sobre A .

  ∑ A     = 0 B x × A B - F × A C = 0 B x × A B = F × A C

Aqui, a reação em B é B x . Substitua 1248 ( h - 2 ) l b f para F e 2 + 26.66 20 × ( h - 2 ) para A C .

9200 × 4 = [ 1248 ( h - 2 ) ] × 2 + 26.66 20 × ( h - 2 ) 36800 = [ 1248 ] × 2 ( h - 2 ) + 26.66 20 36800 1248 = 2 ( h - 2 ) + 26.66 20 29.487 = [ 2 ( h - 2 ) + 1.333 ] 2 ( h - 2 ) = 29.487 - 1.333 2 ( h - 2 ) = 28.157 h = 2 + 28.157 2   = 2 + 14.077   = 16.077 f t

Assim, a profundidade da água é 16.08 f t .

Resposta

h = 16.077 f t

Exercícios de Livros Relacionados

Um tanque cúbico tem as medidas 3 × 3 × 3 m e está cheio com camadas de 1 metro de fluido de densidade 1,0; 1 metro de fluido com d = 0,9 e 1 metro de fluido com d = 0,8. Despreze a pressão atmosféric
Um tanque de água ( d = 1,0 ) tem uma comporta em sua parede vertical com 5 m de altura e 3 m de largura. O topo da comporta está 2 m abaixo da superfície. Qual é a força hidrostática sobre a comporta
No problema F E 2.5 , a que distância abaixo da superfície está o centro de pressão da força hidrostática??
Em líquidos “macios” (módulo de elasticidade volumétrica β baixo), pode ser necessário levar em conta a compressibilidade do líquido em cálculos hidrostáticos. Uma relação aproximada da massa específi
A válvula de retenção abaixo cobre uma abertura com diâmetro de 22,86 cm em uma parede inclinada. A articulação está a 15 cm da linha de centro, como mostrado. A válvula abrirá quando o momento na art