Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas para exames de fundamentos de engenharia - Ex. 6

No problema F E 2.5 , a que distância abaixo da superfície está o centro de pressão da força hidrostática??

Passo 1

Bom, não podemos fazer nada sem pelo menos lembrar o que raios aconteceu no tal do exercício FE2.5, então vamos retomar o desenho feito no cujo dito e ver o que encontramos na ocasião:

Tínhamos um tanque, com a seguinte configuração:

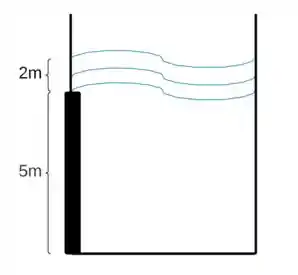
E partindo desse desenho, encontramos a profundidade do Centróide dessa comporta:

h C G = 4,5 m

E então pudemos encontrar uma força hidrostática de:

F = 661   k N

Passo 2

Beleza, agora o que esse cara pede pra gente é o centro do ponto de pressão da água sobre a comporta.

Legal, a gente cancula as coordenadas desse ponto da seguinte forma:

y C P = - I x x s e n θ h C G   A c o m p o r t a

E

x C P = - I x y s e n θ h C G   A c o m p o r t a

Belezura! A única coisa que não sabemos aí é esse tal I x x e I x y . Mas podemos facilmente encontrar eles, lembrando que eles representam o momento de inércia e o produto de inércia da placa.

Como nossa comporta é retangular:

I x y = 0

Enquanto que:

I x x = L a r g u r a   . A l t u r a 3 12

Passo 3

Lembrando que no enunciado do exercício FE2.5 ele nos diz que a comporta tem 5 m   de altura por 3 m de largura. Ficou muito fácil né?!

I x x = 3 5 3 12 = 31,25   m 4

Retomando então na fórmula:

y C P = - ( 31,25 ) s e n ( 90 ) ( 4,5 )   ( 15 )

Lembrando que o θ representa a inclinação de uma placa qualquer em relação à superfície da água... portanto no nosso caso θ = 90 ° , concorda?!

Muito tranquilo então:

y C P = - 0,463 m

Ufa... acabou então né?!! Naaaadaa disso.... o enunciado pede a profundidade desse ponto de pressão.

Se você se lembrar, esse tal y C P mede a distância no eixo y do centro de pressão até o centróide da placa. Entendeu nada?? Tudo bem, vê se a imagem da comporta ajuda a clarificar:

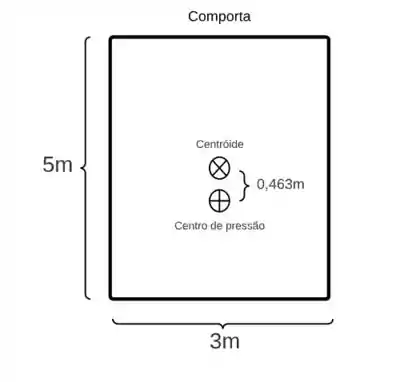
Pegou a idéia?? Isso significa então que a profundidade do centro de pressão é:

h C P = 0,463 + h C G = 0,463 + 4,5 = 4,96 m

Risca mais um da lista!! E bora pro próximo!!!

Resposta

Portanto, Alternativa e   4,96 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um grande bloco de gelo cúbico flutuando na água do mar. As densidades do gelo e da água do mar são 0,92 e 1,025, respectivamente. Se uma parte com 10 cm de altura do bloco de gelo ficar aci
Um muro de arrimo contra um deslizamento de lama deve ser construído colocando-se blocos de concreto retangulares de 0,8 m de altura e 0,2 m de largura ( ρ = 2700k g / m 3 ) lado a lado, como mostra a
Repita o Problema 3-61 para blocos de concreto com 0,4 m de largura.
Repita o Problema 3-63 para um raio de 4 m para a comporta.
Uma comporta na forma de um quarto de círculo e 4 m de comprimento, com raio de 3 m e peso desprezível está ligada com dobradiças à sua aresta superior A , como mostra a Figura P3-63. A comporta contr