Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 73

In Fig. P10.69, let y1 5 6 ft and the gate width b 5 8 ft.

Find the gate opening H that would allow a free-discharge

fl ow of 30,000 gal/min under the gate.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Desenhando o fluxo de água pelo portão

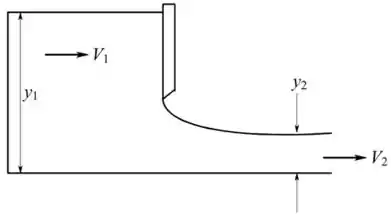
Passo 2

Converta a taxa de fluxo de volume g a l / m i n de para f t 3 / s :

Q   = 30000 g a l / m i n 0.1336 f t 3 1 g a l 1   m i n 60   s   = 66.84 f t 3 / s

Escreva a equação para a descarga através de canal largo:

Q = C d H b 2 g y 1

Aqui, H é a altura de abertura, C d é o coeficiente de descarga, é a b largura do canal, é a g aceleração devido à gravidade, e y 1 profundidade da água a montante.

Q = C d H b 2 g y 1 66.84 = C d H × 8 × 2 × 32.2 × 6 H = 0.425 C d … …  (1) 

Passo 3

Escreva a equação para o coeficiente de descarga:

C d = 0.61 1 + 0.61 H / y 1

Substituindo 6 ft para y 1 .

C d   = 0.61 1 + 0.61 × H / 6   = 0.61 1 + 0.102 H

Passo 4

Substitua 0.61 1 + 0.102 H para C d na equação (1):

H   = 0.425 C d   = 0.425 0.61 1 + 0.102 H   = 0.425 1 + 0.102 H 0.61

Elevando ao quadrado de ambos os lados da equação acima.

0.61 2 H 2 = 0.425 2 ( 1 + 0.102 H ) 0.372 H 2 - 0.018 H - 0.181 = 0

Resolva a equação acima para H .

H = 0.72 f t    or    H = - 0.67   m

Uma vez que apenas o valor positivo é considerado. Portanto, a altura de abertura do portão é 0.72 f t .

Resposta

H = 0.72 f t

Exercícios de Livros Relacionados

Deseja-se medir a vazão em um canal retangular em asfalto de 1,5 m de largura, projetado para escoamento uniforme a uma profundidade de 70 cm e uma inclinação de 0,0036. Os lados verticais do canal tê
A Figura PA10.5 mostra um modelo hidráulico de um vertedouro composto, que combina duas formas diferentes. (a) Excluindo a medição, para a qual ele pode ser inadequado, qual poderia ser a razão de eng
A Figura PA10.6 mostra um escoamento horizontal de água através de uma comporta de fundo, um ressalto hidráulico e sobre um vertedouro de soleira delgada de 1,8 m. Canal, comporta, ressalto e vertedou
Na Figura P10.69, suponha que y 1 = 1,4m e a comporta esteja levantada de maneira que a abertura seja de 15 cm. Calcule a vazão resultante por unidade de largura e a profundidade a jusante.
Na Figura P10.69, seja y 1 = 95c mey 2 = 50c m . Calcule a vazão por unidade de largura se a energia cinética a montante for (a) desprezada e (b) incluída.