A Figura PA10.5 mostra um modelo hidráulico de um vertedouro composto, que combina duas formas diferentes. (a) Excluindo a medição, para a qual ele pode ser inadequado, qual poderia ser a razão de engenharia para o uso desse tipo de vertedouro? (b) Para o rio protótipo, considere que ambas as seções tenham lados com ângulo de 70° em relação à horizontal, tendo a seção do fundo uma base de 2 m de largura e a seção superior uma largura de 4,5 m, incluindo a parte recortada. As alturas das seções horizontais inferior e superior são 1 m e 2 m, respectivamente. Use estimativas de engenharia para fazer um gráfico da profundidade da água a montante em função da vazão do Rio Petaluma no intervalo de 0 a 4 m3/s. (c) Para qual vazão do rio a água transbordará por cima da barragem?
Passo 1
A letra (a) nos pergunta qual poderia ser a razão de engenharia para o uso desse tipo de vertedouro.
Bem, ao usarmos o vertedouro composto com uma parte inferior mais estreita é para manter uma profundidade razoável a montante a uma baixa vazão, além de manter uma profundidade menor em altas vazões. Isso também permite medições mais precisas em vazões baixas.
Passo 2
A letra (b) nos pede pra considerar um vertedouro composto que tenha ambos os lados com ângulo de 70° relação à horizontal, tendo a seção do fundo uma base de 2 m de largura e a seção superior uma largura de 4,5 m.
Além disso, Aa alturas das seções horizontais inferior e superior são 1 m e 2 m, respectivamente, como nessa imagem esquemática que fizemos:
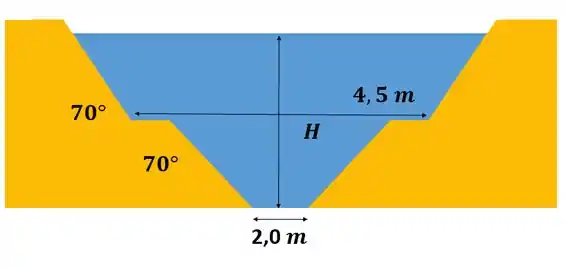
Como não temos uma fórmula específica pra esse tipo de vertedouro, vamos considera-lo um retângulo com contração lateral, com a equação dada na Tabela 10.2b, encontrada na página 742:
Vamos dividir então o problema entre o trapézio de baixo e o trapézio do alto da figura. Vamos descobrir uma largura média pra cada um deles e usar pra calcular a vazão volumétrica pra cada um.
Primeiro, pro trapézio de baixo. Usando algumas relações trigonométricas simples, a gente consegue descobrir que a base maior do trapézio de baixo mede . Ou seja, .
Vamos ter uma vazão de:
Como a letra (b) pede pra gente plotar um gráfico de variando de a , pelo valor de vazão pro trapézio que a gente calculou, sabemos que o nível não vai passar de .
Podemos usar na equação pra vazão e plotar um gráfico de em função de :
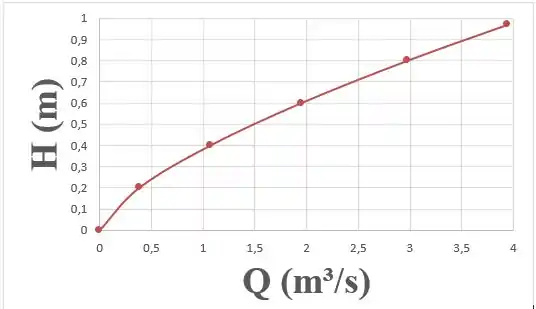
Passo 3
Pra finalizar a questão, devemos resolver a letra (c) e calcular pra qual vazão a água do rio vai transbordar a barragem.
Bem, vamos então calcular pro trapézio de cima. Usando novamente algumas relações trigonométricas simples, a gente consegue descobrir que a base maior do trapézio de cima mede . Ou seja, .
Além disso, devemos considerar apenas considerando o trapézio de cima, pois a altura total da barragem é de .
Vamos então ter uma vazão de:
Agora podemos calcular a vazão total somando as vazões das duas partes da barragem:
Ou seja, pra essa vazão o rio irá transbordar acima da barragem.
Pronto, matamos a questão juntos!

Resposta
(b)
(c) A vazão do rio vazão que fará a água transbordar por cima da barragem é