Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas Abrangentes - Ex. 4

Deseja-se medir a vazão em um canal retangular em asfalto de 1,5 m de largura, projetado para escoamento uniforme a uma profundidade de 70 cm e uma inclinação de 0,0036. Os lados verticais do canal têm 1,2 m de altura. Considere o uso de um vertedouro retangular de placa fina, com largura total ou parcial (Tabela 10.2a, b) para essa finalidade. Sturm [7, p,51] recomenda, para uma correlação precisa, que um vertedouro desses tenha Y ≥ 9 cm e H/Y ≤ 2,0. Determine a viabilidade de instalar um vertedouro desses que tenha precisão e não faça a água transbordar pelos lados do canal

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos um canal retangular de largura b = 1,5   m , constituído por asfalto ( n   =   0,016 ), com declividade S 0 = 0,0036 , e uma profundidade de 0,7   m . Os lados veticais do canal têm 1,2   m de largura, como mostra a imagem ilustrativa abaixo:

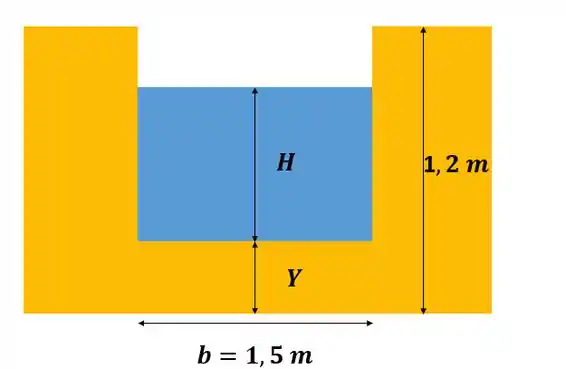
O enunciado nos pede então pra determinar as dimensões de um vertedouro a ser instalado nesse canal, respeitando as restrições de Y   ≥   0,09   m e   H / Y   ≤   2,0 .

Pra calcular essas dimensões vamos usar a equação pra um retângulo com contração lateral, dada na Tabela 10.2b, encontrada na página 742:

Q = 0,581 b - 0,1 H g 1 / 2 H 3 / 2

No próximos passos a gente vai calcular essas dimensões, então vem comigo resolver esse problema!

Passo 2

Pra começo de conversa, temos que descobrir qual a vazão Q necessária pra anter o escoamento no canal.

Pra calcular essa vazão, utilizamos a equação 10.19, apresentada na página 714:

Q = 1 n A R h 2 / 3 S 0 1 / 2

Q = 1 0,016 1,5   m 0,7   m 1,5   m 0,7   m 1,5   m + 2 0,7   m 2 3 0,0036 1 / 2

Q = 2,0 m 3 s

Passo 3

Com o valor de Q = 2,0   m 3 / s , podemos resolver a equação que eu te mostrei no Passo 1 e achar H :

Q = 0,581 b - 0,1 H g 1 / 2 H 3 / 2

2,0 m 3 s = 0,581 1,5   m - 0,1 H 9,81   m / s ² 1 / 2 H 3 / 2

H = 0,845   m

Agora, vamos então determinar um valor de Y . Nossa primeira restrição diz que devemos ter Y   ≥   0,09   m . No entanto, utilizando Y = 0,09   m , a gente chega a H / Y   = 9,4 , o que viola nossa segunda restrição.

Vamos tentar baixar um pouco o valor de Y . Sabemos que o canal tem 1,2   m . Se fizermos 1,2 - 0,845 , obtemos 0,355   m . Vamos tomar Y como sendo um pouco menor que isso, ou seja Y = 0,35   m .

Dessa maneira, o valor de Y vai respeitar o valor da altura máxima do canal de teremos H / Y   = 2,4 , bem mais próximo de nossa segunda restrição, ainda que estejamos violando a segunda.

Ou seja, podemos encontrar valores razoáveis pra aplicação desse projeto, ainda que estejamos violando um pouco nossas restrições.

Pronto, matamos a questão juntos!

Resposta

Determinamos H = 0,845   m e Y = 0,35   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando uma análise do tipo Bernoulli semelhante à da Figura 10.16a, mostre que a vazão teórica do vertedouro em formato de V na Figura P10.118 é dada por Q = 0,7542 g 1 / 2 tan ⁡ α H 5 / 2
Um dispositivo popular para medir vazão na agricultura é a calha Parshall [33], Figura P10.117, que recebeu esse nome em homenagem ao seu inventor, Ralph L. Parshall, que a desenvolveu em 1922 para o
PP10.1 – Um canal reto em terra com vegetação rasteira tem um formato trapezoidal da Fig. 10.7, com b = 4 m e θ = 35°. O canal tem uma declividade de fundo constante de 0,001. A vazão varia sazonalmen
PP10.2 – A barragem Caroselli no Rio Pawcatuck tem 3 m de altura, 27,4 m de largura e a borda aguda. A companhia Coakey usa essa altura para gerar potência hidrelétrica e quer mais potência. Eles soli
Figure P10.76 shows a horizontal fl ow of water through asluice gate, a hydraulic jump, and over a 6-ft sharp-crestedweir. Channel, gate, jump, and weir are all 8 ft wide unfinished concrete. Determin